Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Transformações Lineares Geométricas Compostas

Ver Todos os Exercícios

Teoria

Lembra de quando vimos que podemos representar T L s compostas por meio de um produto de matrizes? Então, isso nos vai ser muito útil agora.

Já vimos uma série de transformações geométricas. Sabemos refletir, projetar, rodar e fazer mais um monte de coisas com os vetores.

Mas uma coisa que não vimos foi o que fazer quando queremos fazer mais de uma transformação dessas, tipo rodar e refletir, ou projetar e ampliar, e por aí vai.

Bom, como já devem estar imaginando, basta multiplicarmos as matrizes de cada transformação geométrica, que teremos uma que faz tudo!

É isso aí, podemos criar uma super T L , e é o que vamos fazer agora!

Então vamos construir uma matriz que reflita um vetor pelo plano x = y , gire ele de 90 ° no sentido trigonométrico ao redor do eixo z e divida o tamanho do vetor por 2 , nessa ordem.

Importante: Percebam que como vamos fazer um produto de matrizes, a ordem é importantíssima. Como já sabemos, quando se trata de matrizes a ordem do produto normalmente importa.

Bom, vamos achar as matrizes que fazem essas coisas então! Eu não falei lá em cima, mas podem considerar que estamos no R 3 haha.

Bom, primeiro a matriz M que reflete os vetores pelo plano x = y :

Ela troca as coordenadas x e y e mantém inalteradas as coordenadas z . Fiz uma imagem 3D e uma de cima pra não ter chance de você não entender haha

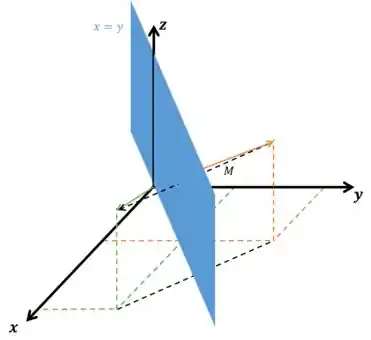
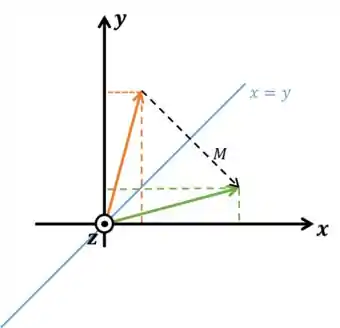
Aplicando a transformação na base canônica do R 3 :

M 1,0 , 0 = 0,1 , 0

M 0,1 , 0 = 1,0 , 0

M 0,0 , 1 = 0,0 , 1

Logo,

M = 0 1 0 1 0 0 0 0 1

Agora vamos achar a matriz R que gira o vetor de 90 ° em torno do eixo z . Essa, já tá até pronta pra gente.

A rotação de θ em torno do eixo z é dada por:

cos ⁡ θ - sen ⁡ θ 0 sen ⁡ θ cos ⁡ θ 0 0 0 1

Logo,

R = cos ⁡ 90 ° - sen ⁡ 90 ° 0 sen ⁡ 90 ° cos ⁡ 90 ° 0 0 0 1

E, finalmente, calculamos a matriz D que divide o vetor por 2 :

D 1,0 , 0 = 1 2 , 0,0

D 0,1 , 0 = 0 , 1 2 , 0

D 0,0 , 1 = 0,0 , 1 2

D = 1 2 0 0 0 1 2 0 0 0 1 2

Finalmente, vamos fazer o produto. Agora é importante prestar atenção na ordem das matrizes! A que vamos aplicar primeiro fica sempre mais a direita no produto (mais próxima do vetor)! Se aplicássemos essas matrizes em um vetor v ficaria algo assim:

D × R × M × v

Logo, a matriz S que queremos ( S de super matriz haha) é dada por:

S = 1 2 0 0 0 1 2 0 0 0 1 2 × 0 - 1 0 1 0 0 0 0 1 × 0 1 0 1 0 0 0 0 1 = - 1 2 0 0 0 1 2 0 0 0 1 2

Ué, só isso? Sim, só isso haha. Vamos aplicar por exemplo o vetor 2,3 , - 3 nela? Bom, o que queremos que saia?

Refletindo ele pelo plano x = y temos o vetor 3,2 , - 3

Rodando de 90 ° no sentido trigonométrico em torno do eixo z , obtemos o vetor - 2 , 3 , - 3

Perceba que essas últimas duas transformações não alteram as coordenadas z ;)

Por fim, dividimos o vetor por 2 e chegamos a - 1 , 3 2 , - 3 2

Agora vamos aplicar nosso vetor na matriz:

- 1 2 0 0 0 1 2 0 0 0 1 2 × 2 3 - 3 = - 1 3 2 - 3 2

E é isso aí galera, já podem brincar de montar matrizes que façam várias coisas! Ou não né, vocês devem ter mais o que fazer haha.

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Queremos projetar um vetor em R 3 sobre o plano y = z , rotacioná-lo de 45 ° em torno do eixo z e, por fim, refletí-lo em torno do plano z = 0 . Sabe-se que as transformações que realizam essas operações são, respectivamente:

P x , y , z = 1 2 x 2 , y + z , y + z  

R x , y , z = 1 2 x - y , x + y , z 2

M x , y , z = x , y , - z

Qual das seguintes matrizes realiza as operações nas ordens pedidas?

a   S = 1 0 0 0 1 2 1 2 0 1 2 1 2   × 1 2 - 1 2 0 1 2 1 2 0 0 0 1 × 1 0 0 0 1 0 0 0 - 1

b   S = 1 0 0 0 1 2 1 2 0 1 2 1 2 × 1 2 1 2 0 - 1 2 1 2 0 0 0 1 × 1 0 0 0 1 0 0 0 - 1

c   S = 1 0 0 0 1 0 0 0 - 1 × 1 2 - 1 2 0 1 2 1 2 0 0 0 1 × 1 0 0 0 1 2 1 2 0 1 2 1 2

d   S = 1 0 0 0 1 0 0 0 - 1 × 1 2 1 2 0 - 1 2 1 2 0 0 0 1 × 1 0 0 0 1 2 1 2 0 1 2 1 2

Passo 1

Ufa, que bom que já deram as T L s pra gente, facilita bastante haha. Vamos começar pela matriz P que projeta o vetor:

P 1,0 , 0 = 1,0 , 0

P 0,1 , 0 = 0 , 1 2 , 1 2

P 0,0 , 1 = 0 , 1 2 , 1 2

Logo:

P = 1 0 0 0 1 2 1 2 0 1 2 1 2

Passo 2

Agora a matriz R que rotaciona:

R 1,0 , 0 = 1 2 , 1 2 , 0

R 0,1 , 0 = - 1 2 , 1 2 , 0

R 0,0 , 1 = 0,0 , 1

Sendo assim:

R = 1 2 - 1 2 0 1 2 1 2 0 0 0 1

Passo 3

Por fim, temos que achar a matriz M :

M 1,0 , 0 = 1,0 , 0

M 0,1 , 0 = 0,1 , 0

M 0,0 , 1 = 0,0 , - 1

Dessa forma,

M = 1 0 0 0 1 0 0 0 - 1

Passo 4

Agora basta prestarmos atenção na ordem da multiplicação! A ordem de precedência é da direita para a esquerda.

Como queremos projetar P →   rotacionar ( R ) →   refletir M , faremos:

S = M × R × P = 1 0 0 0 1 0 0 0 - 1 × 1 2 - 1 2 0 1 2 1 2 0 0 0 1 × 1 0 0 0 1 2 1 2 0 1 2 1 2

Então, a resposta é a letra c

Resposta

Letra c

Exercício Resolvido #2

Elaboração Própria

Determine a matriz da T L T : R 2 → R 2 , reflexão pela origem, seguida de rotação de 45 ° no sentido trigonométrico.

Passo 1

Beleza, vamos começar dando nome aos bois. Nossa matriz de reflexão será a matriz M e a de rotação será a R . Queremos encontrar a matriz T = R × M .

Passo 2

Sabemos que:

M 1,0 = - 1,0

M 0,1 = 0 , - 1

Logo,

M = - 1 0 0 - 1

Passo 3

A matriz de rotação no sentido anti-horário no R 2 é dada por:

cos ⁡ θ - sen ⁡ θ sen ⁡ θ cos ⁡ θ

Substituindo θ por 45 ° :

R = 2 2 - 2 2 2 2 2 2

Passo 4

Agora é só multiplicar:

T = R × M = 2 2 - 2 2 2 2 2 2 × - 1 0 0 - 1 = - 2 2 2 2 - 2 2 - 2 2

Resposta

T = - 2 2 2 2 - 2 2 - 2 2

Exercícios de Livros Relacionados

Seja T x , y , z = 2 x + y , x + y + z , y - 3 z de R 3 em R 3 com produto interno canônico.Mostre que T é um operador auto-adjunto mas não ortogonal.Se v = ( 2 , - 1,5 ) e w = ( 3,0 , 1 ) , verifique
Seja V um espaço vetorial real de dimensão n , T : V → V um operador linear auto-adjunto e v ∈ V um autovetor de T .Mostre que [ v ] , o espaço gerado por v , é invariante por aplicação do aperador T
Seja o operador linear T :R 3 → R 3 cuja matriz em relação à base canônica é 1 4 2 4 - 5 - 4 2 - 4 1 Exiba uma base ortonormal de autovetores.
Dada a matriz A = a 0 0 0 b c 0 c b Mostre que os autovalores são: a ,b + ceb - c Ache uma base de autovetores
Mostre que se T é uma transformação ortogonal do plano no plano, sua matriz em relação à base canônica só pode ser da forma: A = cos ⁡ α - s e nα s e nα cos ⁡ α Ou da forma: B = cos ⁡ α s e nα s e nα