Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

TL Composta

Ver Todos os Exercícios

Teoria

Introdução

Lembra no Ensino Médio que nós podíamos fazer composição de funções? Tipo botar uma dentro da outra e criar uma nova?

Por exemplo, Imagine que a f ( x ) = x ²     e     g ( x ) = x + 3 , então:

( g ∘ f ) ( x ) = g ( f ( x ) )

( g ∘ f ) ( x ) = g ( x ² )

( g ∘ f ) ( x ) = x ² + 3

Lembrou?

Então, como transformações lineares também são funções, podemos fazer composições delas com outras transformações!

Portanto, a definição acima também se aplica a transformações lineares.

Mas aí surge uma questão importante...

Será que se compormos duas T L ' s , a composta gerada a partir das duas ainda é linear?

A resposta é sim! Temos até um teorema para isso haha.

Antes de mais nada é importante lembrar que uma transformação ser linear significa que ela é um tipo particular de função entre dois espaços vetoriais que preserva as operações de adição vetorial e multiplicação por escalar, beleza?!

Bom, a primeira coisa que você tem que reparar é que o contradomínio da T L que vai ficar dentro tem que ser igual ao domínio de fora! Perceba:

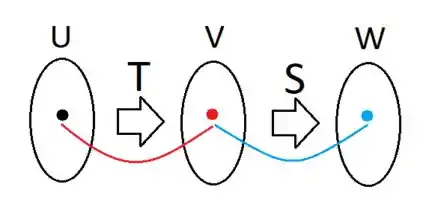
Se você tem T : U → V e S : V → W . A T L composta deve ser S T u . A transformação T levará o vetor u ∈ U em um vetor v ∈ V . A transformação S , por sua vez pegará esse vetor v ∈ V e levará em um vetor w ∈ W . É desse jeito que teremos a S ∘ T :

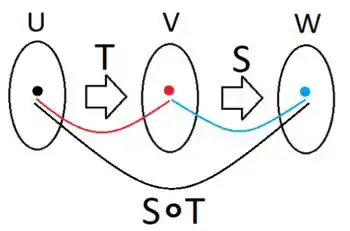
Se o contradomínio de T fosse diferente do domínio de S ia dar ruim, sacou?

Tá beleza, mas como faço isso na prática? Vamos pegar, por exemplo, essas transformações abaixo:

T : R 2 ⟶ R 3

T x , y = ( 2 y , x + y , x - y )

S : R 3 ⟶ R 2

S x , y , z = ( x + y + z ,   2 y - x )

Como o contradomínio de   T é igual ao domínio de S , podemos compor as duas aplicando o resultado da transformação T em S :

S T x , y = S 2 y , x + y , x - y = ( 2 y + x + y + x - y , 2 x + y - 2 y )

Com isso, fazendo as contas, podemos ver que:

S ∘ T : R 2 ⟶ R 2

( S ∘ T ) x , y = ( 2 y + 2 x , 2 x )

E assim temos a nossa expressão da transformação composta.

Acontece que temos outro jeito de achar a TL composta, a partir das matrizes que representam as transformações.

Matriz que Representa uma TL Composta

Vamos supor que agora o enunciado do problema, ao invés de nos dar essas duas transformações com suas expressões analíticas, nos dá as matrizes que as representam.

T x , y = 0 2 1 1 1 - 1 x y

S x , y , z = 1 1 1 - 1 2 0 x y z

E agora, vamos ter que achar as expressões e fazer o mesmo processo de antes?

Não!! Quer dizer, se você quiser, vá em frente que vai dar certo, maaaas, temos um jeito muito mais simples de achar a TL Composta. É só multiplicarmos as 2 matrizes! Mas cuidado, a ordem da multiplicação é muito importante.

Se quisermos fazer S ∘ T a matriz que representa a transformação será ST. Isso acontece porque essa multiplicação de matrizes fica assim:

S ∘ T x , y = 1 1 1 - 1 2 0 0 2 1 1 1 - 1 x y

Reparem que o vetor x , y   está sendo aplicado primeiro na matriz da transformação   T e o resultado disso será aplicado na matriz S . Isso é exatamente o que fizemos quando usamos as expressões analíticas e por isso a ordem da multiplicação não pode ser alterada.

Então, multiplicando S e T , a matriz   S ∘ T será:

S ∘ T x , y = 1 1 1 - 1 2 0 0 2 1 1 1 - 1 x y

S ∘ T x , y = 2 2 2 0 x y

Se você pegar a expressão que achamos lá em cima e achar a matriz da TL vai ver que deu a mesma coisa!

Viu? Agora basta saber as matrizes de cada uma das transformações. Assim, a fórmula dessa composição aplicada nas coordenadas de um vetor, ficaria:

T ∘ S u ξ = T ∘ S ξ ← β ∙ u β ⇒

T ∘ S u ξ = T ξ ← γ ∙ S γ ← β ∙ u β

Sendo β a base do domínio e ξ a base do contradomínio.

Show de bola?! Vamos praticar?

Matriz que Representa uma TL Composta

Exercícios Resolvidos

Exercício Resolvido #1

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 221. – 42

Sejam S e T operadores lineares de R 2 definidos por S x , y = x - 2 y , y e T x , y = 2 x , - y . Determinar:

(a)   S + T

(b)   T - S

(c)   2 S + 4 T

(d)   S ∘ T

(e)   T ∘ S

(f)   S ∘ S

Passo 1

Essa questão é simplesmente jogar uma dentro da outra ou fazer operações com elas, então vou direto ao ponto ok?

Passo 2

a

S + T = S x , y + T x , y = x - 2 y , y + 2 x , - y = 3 x - 2 y , 0

Passo 3

b

T - S = T x , y - S x , y = 2 x , - y - x - 2 y , y = x + 2 y , - 2 y

Passo 4

c

2 S + 4 T = 2 S x , y + 4 T x , y = 2 x - 2 y , y + 4 2 x , - y =

= 2 x - 4 y , 2 y + 8 x , - 4 y = 10 x - 4 y , - 2 y

Passo 5

d

S ∘ T = S T x , y = S 2 x , - y = 2 x - 2 - y , - y = 2 x + 2 y , - y

Passo 6

e

T ∘ S = T S x , y = T x - 2 y , y = 2 x - 2 y , - y = 2 x - 4 y , - y

Passo 7

f

S ∘ S = S S x , y = S x - 2 y , y = x - 2 y - 2 y , y = x - 4 y , y

Resposta

a   3 x - 2 y , 0

b   x + 2 y , - 2 y

c   10 x - 4 y , - 2 y

d   2 x + 2 y , - y

e   2 x - 4 y , - y

f   x - 4 y , y

Exercício Resolvido #2

Lista 1 de Álgebra Linear I para a p2, exercício 12-b), 2015.1, PUC-RIO, Adaptado.

Sabendo que:

T 1 - x = 1 0 0 - 1

T 1 + x = 1 0 0 1

T x 2 = - 1 1 - 1 2

S : R 3 ⟶ P 2

S w , y , z = w + y + 2 w x + z + y x 2

a   Calcule T ( a + b x + c x 2 )

b   Calcule T ∘ S

Passo 1

a   Caramba, polinômios, vetores e matrizes juntos!! E agora???!!

Relaxa, é só seguir os mesmos passos, só que com vetores, e lembrando como se trabalha com polinômios.

Primeira coisa a fazer é a nossa boa e velha combinação linear de uma base do nosso domínio. Como T : P 2 → M 2 × 2 , uma base para ele seria:

β = { 1 - x , 1 + x , x 2 }

Então, podemos fazer uma C L desses elementos para gerar nosso elemento genérico, que é a + b x + c x 2 :

a + b x + c x 2 = α 1 1 - x + α 2 1 + x + α 3 x 2

Passo 2

Agora vamos aplicar T dos dois lados:

T a + b x + c x 2 = T ( α 1 1 - x + α 2 1 + x + α 3 x 2 )

Como T é linear, podemos abrir a expressão do nosso lado direito da equação:

T a + b x + c x 2 = α 1 T 1 - x + α 2 T 1 + x + α 3 T ( x 2 )

E aplicando as informações do enunciado:

T a + b x + c x 2 = α 1 1 0 0 - 1 + α 2 1 0 0 1 + α 3 - 1 1 - 1 2       ( I )

Passo 3

Po, mas ainda tem esses α 1 ,   α 2 ,   α 3 atrapalhando a gente. Lembra que se fossem vetores, você tinha que botar esses coeficientes em função de x , y , z (se fosse do R 3 ), porém agora são polinômios, então você tem que botar esses α 1 ,   α 2 ,   α 3 , em função de a , b , c como se fossem x , y , z .

a + b x + c x 2 = α 1 1 - x + α 2 1 + x + α 3 x 2 ⇒

a + b x + c x 2 = α 1 - α 1 x + α 2 + α 2 x + α 3 x 2 ⇒

a + b x + c x 2 = α 1 + α 2 + α 2 - α 1 x + α 3 x 2 ⇒

α 1 + α 2 = a ⇒ α 1 + b + α 1 = a ⇒ 2 α 1 = a - b ⇒ α 1 = a - b 2 α 2 - α 1 = b ⇒ α 2 = b + α 1 ⇒ α 2 = b + a - b 2 ⇒ α 2 = a + b 2 α 3 = c

Passo 4

Após achar os coeficientes α 1 ,   α 2 ,   α 3 , vamos substituir na nossa equação ( I ) :

T a + b x + c x 2 = a - b 2 1 0 0 - 1 + a + b 2 1 0 0 1 + c - 1 1 - 1 2

Fazendo as contas veremos que:

T a + b x + c x 2 = a - b 2 0 0 b - a 2 + a + b 2 0 0 a + b 2 + - c c - c 2 c

T a + b x + c x 2 = a - c c - c b + 2 c

Passo 5

b   Agora que já achamos T , basta compormos ela com S .

Como: S w , y , z = w + y + 2 w x + z + y x 2

Então:

T ∘ S w , y , z = T w + y ⏟ a + 2 w ⏟ b x + z + y ⏟ c x 2

Vamos substituir direitinho termo a termo segundo a fórmula da transformação T que acabamos de achar:

T ∘ S w , y , z = w + y ⏟ a - ( z + y ) ⏟ c z + y ⏟ c - ( z + y ) ⏟ c 2 w ⏟ b + 2 ( z + y ) ⏟ c ⇒

T ∘ S w , y , z = w - z z + y - z - y 2 ( w + z + y )

Resposta

a   T a + b x + c x 2 = a - c c - c b + 2 c

b   T ∘ S w , y , z = w - z z + y - z - y 2 ( w + z + y )

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 221. – 43

Seja a transformação linear:

S : R 3 → R 4 ,   S x , y , z = x + y , z , x - y , y + z

a   Calcular S ∘ T x , y se:

T : R 2 → R 3

x , y → 2 x + y , x - y , x - 3 y

b Determinar a matriz canônica de S ∘ T e mostrar que ela é o produto da matriz canônica S pela matriz canônica T .

Passo 1

a Calculando S ∘ T x , y :

S ∘ T x , y = S T x , y = S 2 x + y , x - y , x - 3 y =

= 2 x + y + x - y , x - 3 y , 2 x + y - x - y ,   x - y + x - 3 y =

= 3 x , x - 3 y , x + 2 y , 2 x - 4 y

Logo:

S ∘ T x , y = 3 x , x - 3 y , x + 2 y , 2 x - 4 y

Passo 2

b Passando S ∘ T x , y para a forma matricial:

S ∘ T x , y = 3 x x - 3 y x + 2 y 2 x - 4 y = 3 0 1 - 3 1 2 2 - 4 x y

Logo:

S ∘ T = 3 0 1 - 3 1 2 2 - 4

Passo 3

Agora passando T para a forma matricial:

T x , y = 2 x + y x - y x - 3 y = 2 1 1 - 1 1 - 3 x y

Então:

T = 2 1 1 - 1 1 - 3

Passo 4

Agora S :

S x , y = x + y z x - y y + z = 1 1 0 0 0 1 1 - 1 0 0 1 1 x y z

Portanto:

S = 1 1 0 0 0 1 1 - 1 0 0 1 1

Passo 5

Finalmente, temos que:

S ∙ T = 1 1 0 0 0 1 1 - 1 0 0 1 1 × 2 1 1 - 1 1 - 3 = 3 0 1 - 3 1 2 2 - 4 = S ∘ T

E fim de papo.

Resposta

a   S ∘ T x , y = 3 x , x - 3 y , x + 2 y , 2 x - 4 y

b   S ∘ T = 3 0 1 - 3 1 2 2 - 4  

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 221. – 44

As transformações S : R 2 → R 3 e T : R 3 → R 2 são tais que S x , y = y , x - y , 2 x + 2 y e T x , y , z = ( x , y ) .

a Sendo B = 1,0 , - 1 , 1,1 , 1 , 1,0 , 0 uma base do R 3 , determinar a matriz S ∘ T B .

b   Determinar T ∘ S B '   e   T ∘ S B ' ' sendo B ' = 1,1 , 0 , - 1 e B ' ' a base canônica.

Passo 1

a O enunciado já definiu uma base para o R 3 , mas não para o R 2 , então vamos usar a base canônica:

A = 1,0 , 0,1

Como queremos S ∘ T B , precisamos achar as matrizes que representam T e S .

Passo 2

Começando por T , aplicamos a transformação aos vetores da base B do domínio R 3 :

T 1,0 , - 1 = ( 1,0 )

T 1,1 , 1 = ( 1,1 )

T 1,0 , 0 = ( 1,0 )

Como estamos usando a base canônica no contra domínio de T , basta jogarmos esses vetores como colunas de uma matriz:

T A ← B = 1 1 1 0 1 0

Passo 3

Agora para S , aplicamos a transformação na base A do domínio R 2 :

S 1,0 = ( 0,1 , 2 )

S 0,1 = ( 1 , - 1,2 )

Passamos esses vetores para a base B do contra domínio R 3 :

0,1 , 2 = a 1,0 , - 1 + b 1,1 , 1 + c 1,0 , 0

a + b + c = 0 ⇒ c = 0 b = 1 - a + b = 2 ⇒ a = - 1

1 , - 1,2 = a 1,0 , - 1 + b 1,1 , 1 + c 1,0 , 0

a + b + c = 1 ⇒ c = 5 b = - 1 - a + b = 2 ⇒ a = - 3

Logo:

0,1 , 2 B = - 1,1 , 0

1 , - 1,2 B = - 3 , - 1,5

Jogando esses vetores como colunas de uma matriz, temos que:

S B ← A = - 1 - 3 1 - 1 0 5

Passo 4

Por fim,

S ∘ T B = S B ← A × T A ← B = - 1 - 3 1 - 1 0 5 × 1 1 1 0 1 0 = - 1 - 4 - 1 1 0 1 0 5 0

Passo 5

b Vamos começar por T ∘ S B ' Dessa vez a base do R 2 foi dada:

B ' = 1,1 , 0 , - 1

Portanto, tomamos como base do R 3 a canônica:

A = 1,0 , 0 , 0,1 , 0 , 0,0 , 1

Passo 6

Primeiro S . Aplicamos a transformação nos vetores da base B ' do domínio R 3 :

S 1,1 = 1,0 , 4

S 0 , - 1 = - 1,1 , - 2

Como estamos usando a base canônica no contra domínio de S , basta jogarmos esses vetores como colunas de uma matriz:

S A ← B ' = 1 - 1 0 1 4 - 2

Passo 7

Agora T . Aplicamos a transformação na base A do domínio R 3 :

T 1,0 , 0 = 1,0

T 0,1 , 0 = 0,1

T 0,0 , 1 = 0,0

Passamos esses vetores para a base B ' do contra domínio R 2 :

1,0 = 1 1,1 + 1 0 , - 1

0,1 = 0 1,1 - 1 0 , - 1

0,0 = 0 1,1 + 0 0 , - 1

Logo:

1,0 B ' = 1,1  

0,1 B ' = 0 , - 1

0,0 B ' = 0,0

Jogando esses vetores como colunas de uma matriz, temos que:

T B ' ← A = 1 0 0 1 - 1 0

Passo 8

Finalmente,

T ∘ S B ' = T B ' ← A × S A ← B ' = 1 0 0 1 - 1 0 × 1 - 1 0 1 4 - 2 = 1 - 1 1 - 2

Passo 9

Força que tá acabando gente! Agora vamos achar T ∘ S B ' ' com a base do R 2 canônica:

B ' ' = 1,0 , 0,1

Novamente, tomamos como base do R 3 a canônica:

A = 1,0 , 0 , 0,1 , 0 , 0,0 , 1

Passo 10

Primeiro S . Como as bases do domínio e do contra domínio são as canônicas, temos:

S x , y = y x - y 2 x + 2 y = 0 1 1 - 1 2 2 x y

Portanto,

S A ← B ' ' = 0 1 1 - 1 2 2

Passo 11

Agora T . Novamente, as bases do domínio e do contra domínio são as canônicas, então:

T x , y , z = x y = 1 0 0 0 1 0 x y z

Logo:

T B ' ' ← A = 1 0 0 0 1 0

Passo 12

Pra terminar,

T ∘ S B ' ' = T B ' ' ← A × S A ← B ' ' = 1 0 0 0 1 0 × 0 1 1 - 1 2 2 = 0 1 1 - 1

Resposta

a   - 1 - 4 - 1 1 0 1 0 5 0

b T ∘ S B ' = 1 - 1 1 - 2

T ∘ S B ' ' = 0 1 1 - 1

Exercícios de Livros Relacionados

Sejam T 1 : M 22 → R e T 2 : M 22 → M 22 as transformações lineares dadas por T 1 A = t r ( A ) e T 2 A = A T .Encontre T 1 ∘ T 2 A com A = a b c d .Você consegue encontrar T 2 ∘ T 1 A ? Explique.
Em cada parte, seja T : R 2 → R 2 a multiplicação por A . Determine se T tem uma inversa; se tiver, encontre. T - 1 x 1 x 2 A = 5 2 2 1 A = 6 - 3 4 - 2 A = 4 7 - 1 3
Seja F o operador linear do R 2 cuja matriz em relação à base B = 1,0 , 1,4 é F B = 1 1 5 1 Determinar a matriz de F em relação à base canônica, usando a fórmula de mudança de base para um operador.
Determinar as matrizes das seguintes transformações lineares em relação às bases canônicas dos respectivos espaços: F ∈ L R 3 , R 2 definida por F x , y , z = x + y , z F ∈ L R 2 , R 3 definida por F
Seja T um operador linear de um espaço vetorial V de dimensão 2 . Se a matriz de T em relação a uma certa base B de V é a b c d Mostrar que T 2 - a + d T + a d - b c I = 0 (operador nulo)