O desenho a seguir ilustra a difusão de gás dentro da vizinhança de uma superfície catalítica lisa. Gases quentes de hidrocarbonetos pesados difundem para a superfície catalítica onde eles são craqueados em componentes mais leves pela reação: , os produtos leves difundem de volta para a corrente de gás.
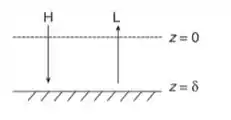
- Reduza a equação diferencial deral de transferência de massa para a reação específica que descreve esse processo no estado estacionário. Liste as hipóteses assumidas para fazer as simplificações.
- Determine a relação da Lei de Fick em termos do componente H e insira isso na equação diferencial obtida na letra (a).
Passo 1
Vamos resolver então a letra a, que ele pede a equação simplificada!
Temos que:
Nossas hipóteses são, pelos dados do problema:
- Estado estacionário
- Sem reação homogênea
- Coordenadas cartesianas
- Fluxo unidimensional no eixo z
A quação simplificada fica então:
Ou seja, nosso fluxo ao longo do eixo z é constante!
Passo 2
Pra letra b o problema quer que a gente relacione a Lei de Fick na expressão que encontramos na letra A. A Lei de Fick é a que descreve o fluxo de massa, então vamos dar uma olhada aqui na expressão que a gente tem:
Abrindo aquele da Lei de Fick:
Agora vamos colocar em termos do nosso problema!
Passo 3
Pela estequiometria temos que , então:
Como na letra (a) encontramos que o fluxo é constante, podemos integrar e colocar N para fora da integral!Integrando então ambos os lados: