A eficácia de produtos farmacêuticos é reduzida pela exposição prolongada a altas temperaturas, à luz e à umidade. Para produtos consumidos que são sensíveis ao vapor de água e encontram-se na forma de comprimidos ou cápsulas e são guardados em ambientes úmidos, como armários de banheiro, embalagens blister são usadas para limitar a exposição direta do medicamento às condições de umidade até o momento imediatamente anterior ao seu uso.
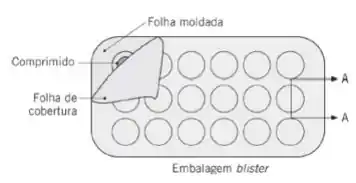
Considere comprimidos que estão contidos em uma embalagem blister composta por uma folha de cobertura plana e uma segunda folha moldada, que tem compartimentos que abrigam cada comprimido. A folha moldada tem espessura e é fabricada com um material polimérico. Cada compartimento tem diâmetro e profundidade . A folha de cobertura é feita de alumínio. O coeficiente de difusão binária do vapor de água no polímero é , enquanto pode-se supor que o alumínio seja impermeável em relação ao vapor de água. Para concentrações molares do vapor de água no polímero nas superfícies externa e interna de e , respectivamente, determine a taxa na qual o vapor de água é transferido através da parede do compartimento para o comprimido.
Passo 1
E aí? Tudo show de bolinhas? Vamos resolver essa questãozinha aí juntinhos? Partiu!!
O nosso enunciado quer a taxa na qual o vapor de água transferido , e para isso nos deu os seguintes dados:
Bom, pra achar a taxa como os dados que temos, vamos fazer algumas considerações, ok?
Estamos trabalhando com um meio estacionário, com fluxo em uma única direção e nesse caso não vamos ter reação química. Além disso como nossa folha polimérica é fininha vamos trabalhar como se fosse uma parede plana.
Passo 2
Para encontrar a taxa de transferência de massa, nessas condições, podemos usar a equação:
Humm… Temos uma área ali, né? Com as considerações que fizemos e o problema que o enunciado nos deu, a nossa taxa de transferência total tem que ser a soma da transferência na parede cilíndrica com a parte circular da base… Opa! então vamos ter duas áreas diferentes:
Somando as duas e substituindo na nossa equação, vamos ter:
Olha que show! Temos tudo que precisamos! Então vamos ao cálculo:
Nossa taxa total de transferência de massa será:
Prontinho! Arrasamos!