2. Calcule o valor da integral da função abaixo para 8 intervalos utilizando os métodos de Simpson e dos Trapézios. Utilize 3 casas decimais e arredondamento padrão.
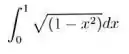
Passo 1
E aí, galera? Neste exercício vamos praticar alguns métodos de integração :) Nós vimos em cálculo 1 como algumas integrais podem ser suuuper difíceis de resolver, então esses métodos podem ser bem úteis na nossa vida!
Considerando intervalos, o método de Simpson aproxima a integral usando a seguinte equação:
, onde:
e .
Pessoal, fiquem bem atentos, hein? Para todo , devemos multiplicar por um fator de 2 no cálculo de . Por outro lado, para , devemos usar um fator de 4.
Já no método dos Trapézios, vamos aproximar a integral usando esta outra equação:
, onde:
e .
Passo 2
De acordo com o enunciado, sabemos que e . Vamos então calcular os fatores e , beleza?
Para calcular , devemos primeiro definir os oito pontos usados na equação, certo? Sabemos que e . Para descobrir os demais pontos, devemos incrementar o valor de ao ponto inicial, até alcançarmos o ponto final! Vamos lá!
Passo 3
Em seguida, vamos obter o valor de para cada um desses pontos:
Ufaaaa! Substituindo na equação de , obtemos, para o método de Simpson:
Portanto:
Agora, para o método dos Trapézios:
Portanto:
E é isso, galera! Até a próxima!
Resposta
Método de Simpson: 0,782
Método dos Trapézios: 0,772