Método de Newton Raphson

Teoria

Fala aí, você acaba de chegar no Responde Aí! E agora vamos bater um papo sobre o Método de Newton Raphson

Método de Newton Raphson

Fórmula do método de Newton Raphson

O método de Newton-Raphson é um tipo de método do ponto fixo que utiliza uma técnica diferente pra refinamento.

O que esse método faz é minimizar o valor da função de iteração no ponto fixo acelerando a convergência do método do ponto fixo.

E como calculamos isso matematicamente?

Pensando em termos de funções que funcionam por iteração e que cada método depende do anterior. A nossa sequência de iteração será:

Convergência do método de Newton Raphson

Geralmente o método de Newton converge desde que nosso palpite inicial seja escolhido “suficientemente próximo” da raiz ξ , satisfazendo as hipóteses de convergência do MPF.

Ou seja, com uma boa escolha de a convergência do método é garantida pelo seguinte teorema

Critério de parada

Basicamente, aplicamos os critérios de convergência e iteração até que o valor de atenda ao critério de parada!

Beleza, nós já vimos qual a função de iteração desse método, e como ele é uma derivação do Método do Ponto Fixo, ele necessita exatamente das mesmas coisas!

Ele precisa de um chute inicial e o critério de parada será:

E, novamente, outro critério usado é:

Prova geométrica do método de Newton Raphson

O método de Newton Raphson também pode ser obtido geometricamente.

Dado o ponto , traçamos a reta tangente à curva neste ponto. A fórmula da reta tangente é dada por:

Essa reta funciona como uma aproximação para a função na vizinhança de . Ou seja, quanto mais próximo de estivermos, melhor a reta tangente aproxima a própria função.

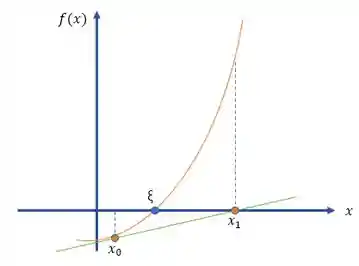
Obtenção geométrica do método de Newton Raphson

E como nosso chute deve estar próximo da raiz de , consideramos a aproximação como uma aproximação boa o suficiente para encontrar o zero de e fazemos:

Exercício

Calcule o valor de pelo método de Newton Raphson usando

Prova geométrica do método de Newton Raphson

Exercício

Exercícios Resolvidos

Exercício Resolvido #1

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 2 adaptado

Seja e . Use o Método de Newton para encontrar . O valor poderia ser usado?

Passo 1

Só aplicar o algoritmo:

Cálculos Iniciais

Taí o nosso .

A próxima pergunta é, poderia ser usado? Não poderia pois a derivada nesse ponto vale :

Isso nos criaria uma indeterminação na nossa função de iteração.

Resposta

Não poderia pois criaria uma indeterminação na nossa função de iteração.

Exercício Resolvido #2

Lista 2 – Professor Mauro – UFRJ – Questão 2

Dê um exemplo de função , que tenha pelo menos uma raiz, onde o Método de Newton-Raphson não converge sempre.

Passo 1

Um exemplo de função para a qual o método de Newton não converge sempre é . A sequência diverge para valores acima de e para valores abaixo de .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6 adaptado

Use o Método de Newton para encontrar soluções com precisão de para os seguintes problemas:

para

para e

Passo 1

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 2

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 3

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 4

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 5

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 6

Intervalo

Cálculos Iniciais

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Como não alcançamos o critério de parada continuamos as iterações.

Iteração :

Critério de Parada:

Alcançamos nosso critério de parada. Então .

Passo 7

Intervalo

Cálculos Iniciais

Método de Newton Raphson

Teoria