Método da Secante
Produzido por Bruno PestanaTeoria
Opa, seja muito bem vindo ao Responde Aí! Bora bater aprender o Método da Secante?!
Método da Secante: Fórmula
O Método da Secante é um método iterativo usado pra encontrar zeros de funções reais. Ele é bem parecido com o Método de Newton-Rapson, mas com uma vantagem… aqui não tem derivada. Então se você pegar uma função cabulosa, difícil de derivar, o método da secante é o melhor caminho! 🤩
Ela tem essa carinha aqui:
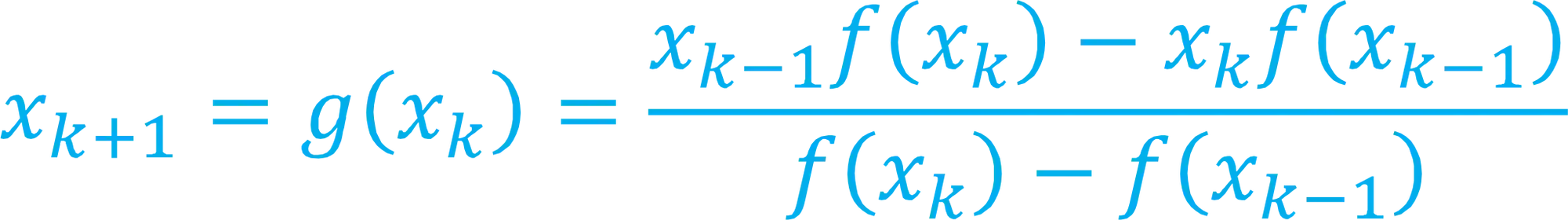
É óbvio que nem tudo são flores…o Método de Newton tem a vantagem de convergir mais rápido! Ou seja, escolha suas batalhas meu caro!
Como podemos ver na fórmula a cima, no método da secante precisamos de dois chutes iniciais
Temos os dois chutes iniciais
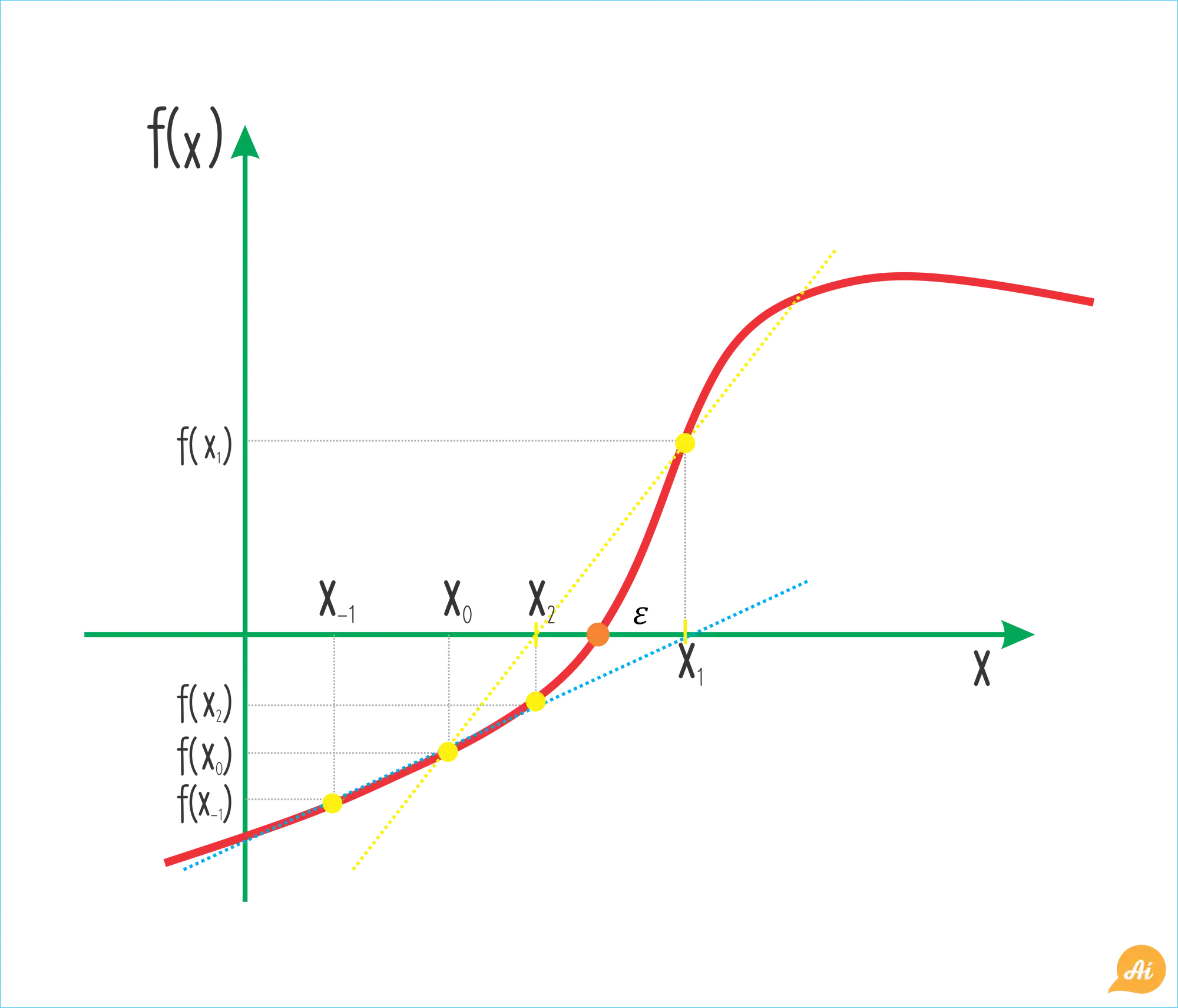
Depois disso fazemos uma outra reta, ligando os pontos
Repetimos esse processo até chegarmos a uma aproximação próxima o suficiente! 😉
📢 Clique para ver mais:
- Método da Bisseção
- Método da Secante: Exercícios Resolvidos
- Método da Posição Falsa
- Método do Ponto Fixo (MPF)
-Beleza, mas como a gente usa o método da secante na prática?! 😖
A gente vai aprender tudo tim tim por tim tim! Mas pra começar com tudo, se liga nesse vídeo aqui 👇
Critério de Parada
Para o método, os critérios de parada mais usados são:
- Seja
uma aproximação da raiz encontrada em alguma iteração, paramos se ; - Seja
a aproximação da raiz na iteração , paramos se .
Pode-se usar vários critérios de uma vez ou apenas um, vai depender do problema que temos que resolver. Além disso, vários outros critérios podem ser usados, esses são só os mais comuns. É sempre recomendável adicionar um número máximo de iterações como critério de parada.
Convergência
Este método é uma aproximação do método de Newton, e tem condições de convergência muito similares! De forma geral, a maioria das vezes em que ele diverge ou demora para convergir é quando
Apesar de ele não ser tão rápido quanto o método de Newton e necessitar de uma aproximação inicial a mais, ele não precisa mais calcular o valor da derivada a cada iteração, podendo ganhar tempo em esforço computacional!
Método da Secante: Algoritmo
Vamos ver como fica o algoritmo do método da secante!
Passo 1: Dados iniciais
Esses são os dados que o programa vai receber de você
- Aproximações iniciais
e ; - Precisão do resultado final
e
Passo 2: Definir um contador de iterações k=0
Esse passo é importante pra sabermos quantas vezes o programa rodou até ele interagir!
Passo 3: Verificamos o primeiro critério de parada
Nesse passo falamos para o programa: Se
Passo 4: Aumentamos uma iteração no contador
Para isso fazemos
Passo 5: Calculamos o x
Para isso usamos a fórmula do método da secante:
Passo 6: Verificamos o segundo critério de parada
Nessa etapa falamos para o programa: Se
Passo 7: Atualizamos o x
Para isso fazemos
Passo 8: Voltamos para o Passo
Prontinho, é isso! Agora vamos praticar com exercícios?!
Critério de Parada
Convergência
Método da Secante: Algoritmo
Exercícios Resolvidos
Exercício Resolvido #1
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 3 adaptado
Seja . Dados e , encontre usando o método da secante.
Passo 1
Só aplicar o algoritmo:
Resposta
Exercício Resolvido #2
Lista 1 – UTFPR – Prof Violeta Stephan – Questão 9
Calcule a raiz real da equação próxima de , por meio do método da secante. Considere .
Passo 1
Sabemos que a raiz está próxima de , então temos nossa primeira aproximação. Vamos encontrar a segunda:
está mais próximo de zero então ele será nosso segundo chute.
Passo 2
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. .
Resposta
Exercício Resolvido #3
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 11 adaptado
Use o método da secante para encontrar soluções com precisão para os seguintes problemas:
para
para
Passo 1
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. . Claro que nós sabemos que o valor correto aqui é né haha, então foi uma boa aproximação.
Passo 2
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. .
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule pelo método da Secante. Considere .
Passo 1
Uma forma de se calcular o valor de é dessa forma:
Passo 2
Agora precisamos de dois chutes iniciais. está em algum lugar entre e . Ou seja, está em algum lugar entre e . Como é bem mais próximo de que de , vamos usar e como aproximações iniciais.
Passo 3
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. .
Resposta
.
Exercício Resolvido #5
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6 adaptado
Use o Método da Secante para encontrar soluções com precisão de para os seguintes problemas:
para
para e
para e
para e
Passo 1
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 2
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 3
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 4
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 5
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 6
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Passo 7
Intervalo
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Alcançamos nosso critério de parada. Então .
Resposta
Intervalo :
Intervalo :
Intervalo :
Intervalo :
Intervalo :
Intervalo :
Intervalo :
Exercício Resolvido #6
Lista 2 – UVA – Questão 6 Adaptada
A recolha de energia solar através da focagem de um campo plano de espelhos numa central de recolha foi estudada por Vant-Hull . A equação para a concentração geométrica do fator é dada por:
em que é o ângulo do campo, é a cobertura da fração do campo com espelhos, é o diâmetro do coletor e é o comprimento do coletor. Considerando , e , calcule o ângulo positivo inferior a para o qual a concentração do fator é . Utilize o método da secante com .
Passo 1
Vamos começar botando valores nessa fórmula:
Passo 2
Temos que . Então vamos usar como aproximações iniciais algo entre e .
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. .
Resposta
Exercício Resolvido #7
Lista 2 – UVA – Questão 7 Adaptada
Um certo equipamento de euros vai ser pago durante anos. O pagamento anual é de euros. A relação entre o custo do equipamento , o pagamento anual , o número de anos e a taxa de juros é a seguinte:
Utilize o método da Secante para determinar a taxa de juros utilizada nos cálculos. O valor da taxa pertence ao intervalo . Use .
Passo 1
Vamos começar botando valores nessa fórmula:
Passo 2
O valor da taxa está no intervalo . Então é só escolhermos números quaisquer nesse intervalo como aproximações iniciais.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. . Ou seja, nossa taxa de juros é de .
Resposta
Juros de
Exercício Resolvido #8
Lista 2 – UNICAMP – 2013 – Questão 9 Adaptada
Considere a função . Obtenha seu ponto crítico com o auxílio do método da secante e precisão . (Obs.: pontos críticos: )
Passo 1
Repare que o problema aqui não é encontrar o zero diretamente de . Ele está pedindo o zero de ! Então basta derivar, igualar a zero e aplicar nosso algoritmo:
Passo 2
Agora precisamos de duas aproximações para a raiz:
Temos uma raiz entre e . Como parece estar mais próximo da raiz vamos usar como aproximações iniciais e .
Passo 3
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Beleza, chegamos ao nosso critério. O ponto crítico é
Resposta
Exercício Resolvido #9
Lista 1 – UTFPR – Prof Violeta Stephan – Questão 14 Adaptada
Um circuito consiste em um resistor , um indutor e um capacitor conectados em série com uma fonte de tensão alternada . A amplitude da corrente é dada por:
onde , a frequência angular, está relacionada à frequência por . Determine para um circuito com , , , e , usando o método da secante com tolerância . Use como critério de parada o valor de .
Passo 1
Substituindo os valores:
Passo 2
Vamos encontrar o intervalo que contém a raiz agora.
Beleza, temos uma raiz no intervalo . Vamos usar como aproximações iniciais e .
Passo 3
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Pronto, chegamos ao nosso critério de parada. A frequência do circuito é de .
Resposta
Exercício Resolvido #10
Lista 2 – UNICAMP – 2013 – Questão 9 Adaptada
Use o método da secante para obter o ponto sobre a curva mais próximo do ponto com precisão de .
Passo 1
Essa questão é bem elaborada, vem comigo. Primeira coisa, como calculamos a distância entre dois pontos? Assim oh:
Temos e . Substituindo:
Queremos minimizar essa distância, certo? E o que fazemos quando queremos achar o máximo ou mínimo de algo? Derivamos e igualamos a zero né??
Po, mas essa raiz aí ta ferrando a gente! Calma, nem tudo tá perdido haha. Tem uma sacada muito boa que podemos ter aqui. Pensa comigo, o mínimo dessa função também não é igual ao mínimo de ? Se pegarmos todos os valores possíveis de e elevarmos ao quadrado, o que nos dá o mínimo de será o mesmo que nos dará o mínimo de ! Então podemos derivar o quadrado de , que é bem mais fácil:
Passo 2
Agora precisamos achar nossas aproximações iniciais:
Temos uma raiz no intervalo . Como está bem mais próximo do vamos usar como chutes e .
Passo 3
Iteração :
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Critério de Parada:
Beleza, chegamos ao nosso critério. O valor de que minimiza a distância é .
O ponto sobre a reta será então:
Resposta