Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Plano Tangente

Ver Todos os Exercícios

Teoria

Plano Tangente

Para funções de uma variável, vimos que, se temos uma curva e derivamos essa curva num determinado ponto, podemos encontrar a reta tangente a essa curva nesse ponto.

Essa reta é aproximadamente igual ao gráfico da função nas proximidades desse ponto. Isso quer dizer que, a medida que vamos dando um zoom no gráfico da função próximo ao ponto de tangencia, a gente não consegue distinguir o que é o gráfico da função e o que é a reta tangente, porque eles são muuuuuuuuuito parecidos.

Agora, em funções de duas variáveis, o raciocínio é totalmente análogo! Basicamente vamos aumentar uma dimensão nas coisas que estamos trabalhando: a curva vai ser uma superfície e a reta tangente será um plano tangente.

Assim, o plano tangente se confunde com o gráfico da função ali pertinho do ponto de tangencia. Igualzinho tínhamos para a reta tangente. Dá uma olhada:

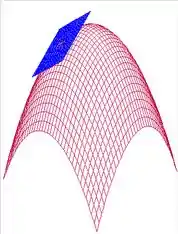
Boa! Agora que a gente já entendeu o que é um plano tangente, vamos aprender a calcular.

Como calcular?

Para calcularmos a equação do plano tangente a uma superfície, precisamos de duas coisas:

  1. um ponto do plano: P 0 = x 0 , y 0 , z 0
  2. um vetor normal ao plano: n →

Equação do plano:

x - x 0 , y - y 0 , z - z 0 ⋅ n → = 0

Mas quem será que vai ser esse vetor normal?

Se ali pertinho do ponto de tangencia o plano e o gráfico da função são praticamente a mesma coisa e sabemos que o vetor gradiente é perpendicular ao gráfico da função, então, é de se esperar que o vetor gradiente também seja perpendicular ao plano tangente!

Então, o vetor normal ao plano tangente será o vetor gradiente!

n → = ∇ F ( P 0 )

Entao ficamos com

x - x 0 , y - y 0 , z - z 0 ⋅ ∇ F ( P 0 ) = 0

E o nosso vetor gradiente é dado desse jeitinho aqui

∇ F P 0 = f x P 0 , f y P 0 , f z P 0

Entao ficamos com

f x P 0 x - x 0 + f y P 0 y - y 0 + f z P 0 z - z 0 = 0

Desse modo, por exemplo, para calcular o plano tangente ao gráfico da função

f x , y = 1 - x 2 - 2 y ²

no ponto

P 0 = ( 1,1 , - 2 )

Vamos seguir o passo a passo:

  1. Caso seja necessário, substituir f ( x , y ) por z na equação da superfície

    2. z = 1 - x 2 - 2 y 2

  2. Jogar todas as variáveis para o lado esquerdo da equação

    3. 0 = z + x 2 + 2 y 2 - 1

  3. Chamar de F x , y , z a expressão deixada no lado esquerdo da equação

    4. F x , y , z = z + x 2 + 2 y 2 - 1

  4. Calcular gradiente de F : ∇ F x , y , z = f x , f y , f z Vamos achar as derivadas parciais, ficando com:

    5. ∇ F x , y , z = 2 x , 4 y , 1

  5. Calcular gradiente de F no ponto P 0 : ∇ F P 0 = ∇ F x 0 , y 0 , z 0

    6. P 0 = 1,1 , - 2 → ∇ F P 0 = ( 2,4 , 1 )

  6. O vetor normal será n → = ∇ F P 0

    7. n → = 2,4 , 1

  7. Substituir na equação do plano:

f x P 0 x - x 0 + f y P 0 y - y 0 + f z P 0 z - z 0 = 0

2 x - 1 + 4 y - 1 + 1 z + 2 = 0

z + 2 + 2 x - 2 + 4 y - 4 = 0

2 x + 4 y + z = 4

Como calcular?

Exercícios Resolvidos

Exercício Resolvido #1

CEFET, Cálculo 2, Listas, Lista 1, Professor Roberto Thomé, questão 14, item c.

Encontrar a equação do plano tangente à superfície no ponto dado:

z = 9 - 5 x 2 - 3 y 2

P = ( 1 , - 1 )

Passo 1

Simples, apenas seguir o nosso passo-a-passo, lembra dele?

  1. Caso seja necessário, substituir f ( x , y ) por z na equação da superfície
  2. Jogar todas as variáveis para o lado esquerdo da equação e achar z 0
  3. Chamar de F x , y , z a expressão deixada no lado esquerdo da equação
  4. Calcular gradiente de F : ∇ F x , y , z
  5. Calcular gradiente de F no ponto P 0 : ∇ F P 0 = ∇ F x 0 , y 0 , z 0
  6. O vetor normal será n → = ∇ F P 0

Passo 2

Já temos f x , y = z , então podemos jogar todas as variáveis para o lado esquerdo:

z - 9 - 5 x 2 - 3 y 2 = 0

Passo 3

Vamos encontrar logo qual é a coordenada z do ponto dado no enunciado? É só a gente substituí-lo na expressão aqui de cima:

z - 9 - 5 x 2 - 3 y 2 = 0

No ponto P = ( 1 , - 1 , z 0 ) :

z 0 - 9 - 5 . 1 2 - 3 . - 1 2 = 0

z 0 - 1 = 0

z 0 = 1

Passo 4

Ok, agora temos que

F x , y , z = z - 9 - 5 x 2 - 3 y 2

Passo 5

Estamos prontos para calcular o vetor gradiente! Lembra da expressão dele?

∇ F x , y , z = F x , F y , F z

Como F x , y , z = z - 9 - 5 x 2 - 3 y 2 , vamos calcular as derivadas parciais

F x x , y , z = 5 x 9 - 5 x 2 - 3 y 2

F y x , y , z = 3 y 9 - 5 x 2 - 3 y 2

F z x , y , z = 1

Passo 6

Assim, nosso vetor gradiente, no ponto dado, P = 1 , - 1,1 , fica:

F x 1 , - 1 , 1 = 5.1 9 - 5.1 2 - 3 . - 1 2 = 5

F y 1 , - 1 , 1 = 3 . - 1 9 - 5.1 2 - 3 . - 1 2 = - 3

F z x , y , z = 1

Então o nosso gradiente será, ∇ F x , y , z = F x , F y , F z

∇ F 1 , - 1,1 = 5 , - 3,1

Passo 7

Agora que temos o gradiente, temos o vetor normal ao plano tangente! Portanto, basta jogarmos na equação do plano e ele aparecerá! Lembra da equação do plano?

x - x 0 , y - y 0 , z - z 0 ⋅ n → = 0

Colocando P = ( 1 , - 1,1 ) e n → = ∇ F 1 , - 1,1 = 5 , - 3,1 teremos nosso plano:

x - 1 , y + 1 , z - 1 ⋅ 5 , - 3,1 = 0

5 x - 5 - 3 y - 3 + z - 1 = 0

5 x - 3 y + z - 9 = 0

Resposta

Plano: 5 x - 3 y + z - 9 = 0

Exercício Resolvido #2

PUC-RJ, Cálculo 2, P2 2013.1, questão 1, item a

Considere a função

f x , y = x 2 - 1 y 2 - 1 ,         x , y ∈ R 2

Encontre os pontos x , y , z do gráfico de f onde o plano tangente é horizontal, isto é, de equação cartesiana z = c ( c constante)

Passo 1

Para acharmos o plano tangente precisamos primeiro achar o vetor normal da função, e antes de qualquer coisa precisamos achar a função F x , y , z substituindo f x , y = z

f x , y = z = x 2 - 1 y 2 - 1

z - x 2 - 1 y 2 - 1 = 0

F x , y , z = z - x 2 - 1 y 2 - 1

Agora vamos achar seu gradiente

∇ F = F x , F y , F z

F x = - y 2 - 1 2 x = - 2 x y 2 - 1

F y = - x 2 - 1 2 y = - 2 y x 2 - 1

F z = 1

O vetor gradiente vai ser

∇ F = - 2 x y 2 - 1 , - 2 y x 2 - 1 , 1

Então o vetor normal vai ser

n → = - 2 x y 2 - 1 , - 2 y x 2 - 1 , 1

Passo 2

O vetor normal do plano z = c vai ser 0,0 , 1 , isso nos diz que as coordenadas x e y de n → precisam ser 0 . E passamos a ter o sistema

- 2 x y 2 - 1 = 0 - 2 y x 2 - 1 = 0

Pela primeira equação temos

x = 0

Ou

y 2 - 1 = 0

Isso nos diz que

x = 0       o u         y = 1         o u         y = - 1

Pela segunda equação temos

y = 0

Ou

x 2 - 1 = 0

Isso nos diz que

y = 0         o u         x = 1           o u           x = - 1

Vamos juntar essas duas possibilidades, vamos ter os pontos

x = 0   e   y = 0 ⇒ z = 0 2 - 1 0 2 - 1 = 1

y = 1   e   x = 1 ⇒ z = 1 2 - 1 1 2 - 1 = 0

y = 1   e   x = - 1 ⇒ z = - 1 2 - 1 1 2 - 1 = 0

y = - 1   e   x = 1 ⇒ z = 1 2 - 1 - 1 2 - 1 = 0

y = - 1   e   x = - 1 ⇒ z = - 1 2 - 1 - 1 2 - 1 = 0

Logo são os pontos

0,0 , 1

1,1 , 0

1 , - 1,0

- 1,1 , 0

- 1 , - 1,0

Resposta

0,0 , 1

1,1 , 0

1 , - 1,0

- 1,1 , 0

- 1 , - 1,0

Exercício Resolvido #3

UFRJ, Cálculo 2, P2 2013.1, questão 1

Considere a superfície S formada pelos pontos x , y , z ∈ R 3 satisfazendo a equação

x y z = e β x

Onde β é um número real.

  1. Escreva a equação do plano tangente a S no ponto P 0 = 3 , 1 3 ,   e 3 β ∈ S
  2. Encontre β de modo que o plano tangente a S no ponto P 0 contenha a origem.

Passo 1

a)

Para o plano tangente primeiro encontrar o vetor n → . Começamos fazendo

x y z = e β x

F x , y , z = x y z - e β x

Vamos agora achar o gradiente de F

∇ F = y z - β e β x , x z , x y

Lembra que o vetor normal é o gradiente substituindo o valor??

n → = 1 3   e 3 β - β e 3 β , 3   e 3 β , 3 ⋅ 1 3

n → = 1 3   e 3 β - β e 3 β , 3   e 3 β , 1

Passo 2

A equação do plano é:

x , y , z ⋅ n → = P 0 ⋅ n →

Substituindo os valores

x , y , z ⋅ 1 3   e 3 β - β e 3 β , 3   e 3 β , 1 = 3 , 1 3 ,   e 3 β ⋅ 1 3   e 3 β - β e 3 β , 3   e 3 β , 1

x 1 3   e 3 β - β e 3 β + 3 y   e 3 β + z = e 3 β - 3 β e 3 β +   e 3 β + e 3 β

x 1 3   e 3 β - β e 3 β + 3 y   e 3 β + z = 3 e 3 β - 3 β e 3 β

Passo 3

b)

Se ele contem a origem então podemos substituir a origem na equação do plano e achar a equação para β

x 1 3   e 3 β - β e 3 β + 3 y   e 3 β + z = 3 e 3 β - 3 β e 3 β

0 1 3   e 3 β - β e 3 β + 3 ⋅ 0   e 3 β + 0 = 3 e 3 β - 3 β e 3 β

0 = 3 e 3 β - 3 β e 3 β

0 = 3 e 3 β 1 - β

Como exponencial é sempre positivo

1 - β = 0

β = 1

Resposta

  1. x 1 3   e 3 β - β e 3 β + 3 y   e 3 β + z = 3 e 3 β - 3 β e 3 β
  2. β = 1

Exercício Resolvido #4

UNICAMP, Cálculo 2, Exame 2014 Tarde, questão 1, item b

Verifique que o elipsoide 3 x 2 + 2 y 2 + z 2 = 9 e a esfera x 2 + y 2 + z 2 - 8 x - 6 y - 8 z + 24 = 0 se tangenciam (ou seja, possuem o mesmo plano tangente) no ponto ( 1,1 , 2 ) .

Passo 1

Nessa questão, fatalmente vamos ter que calcular as equações dos planos tangentes às duas superfícies no ponto ( 1,1 , 2 ) e verificar que são o mesmo plano.

Então que tal a gente começar lembrando a equação do plano tangente ao gráfico de uma função de 3 variáveis f num ponto P 0 ? Podemos escrevê-la dessa forma:

x , y , z ⋅ ∇ f P 0 = P 0 ⋅ ∇ f ( P 0 )

Atenção, esses pontos aí na equação são produtos escalares!

Bem, vamos prosseguir!

Passo 2

Podemos reescrever as equações do elipsoide e da esfera dessa forma:

F x , y , z = 0       e       G x , y , z = 0

Com F x , y , z = 3 x 2 + 2 y 2 + z 2   - 9 e   G x , y , z = x 2 + y 2 + z 2 - 8 x - 6 y - 8 z + 24 .

Passo 3

Vamos começar nos focando no elipsoide, calculando o gradiente da F . As derivadas parciais vão ser:

∂ F ∂ x x , y , z = 6 x + 0 + 0 - 0 = 6 x

∂ F ∂ y x , y , z = 0 + 4 y + 0 - 0 = 4 y

∂ F ∂ z x , y = 0 + 0 + 2 z - 0 = 2 z

Então o gradiente da F   é:

∇ F x , y , z = 6 x , 4 y , 2 z

Mas o que nos interessa nessa questão é o gradiente no ponto ( 1,1 , 2 ) , que é:

∇ F 1,1 , 2 = 6,4 , 4

Passo 4

Show! Agora podemos aplicar a fórmula que vimos antes:

x , y , z ⋅ ∇ F 1,1 , 2 = ( 1,1 , 2 ) ⋅ ∇ F ( 1,1 , 2 )

x , y , z ⋅ 6,4 , 4 = 1,1 , 2 ⋅ ( 6,4 , 4 )

6 x + 4 y + 4 z = 6 + 4 + 8 = 18

Portanto, o plano tangente ao elipsoide 3 x 2 + 2 y 2 + z 2 = 9 no ponto ( 1,1 , 2 ) é:

6 x + 4 y + 4 z = 18

Passo 5

Agora temos que verificar que o plano tangente à esfera x 2 + y 2 + z 2 - 8 x - 6 y - 8 z + 24 = 0 no ponto ( 1,1 , 2 ) é o mesmo!

Para isso, definimos G x , y , z = x 2 + y 2 + z 2 - 8 x - 6 y - 8 z + 24 , lembra?

Então vamos seguir o mesmo procedimento da F , começando pelo gradiente:

∂ G ∂ x x , y , z = 2 x + 0 + 0 - 8 - 0 - 0 + 0 = 2 x - 8

∂ G ∂ y x , y , z = 0 + 2 y + 0 - 0 - 6 - 0 + 0 = 2 y - 6

∂ G ∂ z x , y , z = 0 + 0 + 2 z - 0 - 0 - 8 + 0 = 2 z - 8

Então o gradiente da G é:

∇ G x , y , z = ( 2 x - 8 ,   2 y - 6 ,   2 z - 8 )

E no ponto 1,1 , 2 :

∇ G 1,1 , 2 = 2 - 8 ,   2 - 6 ,   4 - 8 = ( - 6 , - 4 , - 4 )

Observação: já podemos notar que ∇ G 1,1 , 2 = - ∇ F 1,1 , 2 . Poderíamos usar isso pra provar que os planos tangentes são os mesmos, mas vamos continuar do jeito que tá porque já tá quase no fim :D

Passo 6

Aplicando a fórmula do plano tangente, vamos ter:

x , y , z ⋅ ∇ G 1,1 , 2 = ( 1,1 , 2 ) ⋅ ∇ G ( 1,1 , 2 )

x , y , z ⋅ - 6 , - 4 , - 4 = 1,1 , 2 ⋅ ( - 6 , - 4 , - 4 )

- 6 x - 4 y - 4 z = - 6 - 4 - 8 = - 18

Multiplicando tudo por - 1 :

6 x + 4 y + 4 z = 18

É a mesma equação que achamos antes!

O elipsoide 3 x 2 + 2 y 2 + z 2 = 9 e a esfera x 2 + y 2 + z 2 - 8 x - 6 y - 8 z + 24 = 0 possuem o mesmo plano tangente em ( 1,1 , 2 ) , portanto eles se tangenciam.

Resposta

O elipsoide e a esfera têm o mesmo plano tangente em 1,1 , 2 : o plano 6 x + 4 y + 4 z = 18   .

Exercício Resolvido #5

UNICAMP, Cálculo 2, P1 2014 Manhã, questão 3

Determine a equação dos planos tangentes ao gráfico de f x , y = 7 - x 2 - y 2 , que passam, ambos, pelos pontos 1,0 , 7 e 3,0 , 3 .

Passo 1

Bom, equação do plano tangente é aquele mesmo processo de sempre, achar as derivadas parciais (formando o vetor gradiente) e multiplicar por um vetor genérico x - x 0 , y - y 0 ,   z - z 0 . Aí falamos que esse produto é 0 , pois o vetor gradiente e o plano tangente são perpendiculares.

Então partiu encontrar essas derivadas!

f x , y = z = 7 - x 2 - y 2

Então,

F x , y , z = 7 - x 2 - y 2 - z

f x x , y = - 2 x

f y x , y = - 2 y

f z x , y = - 1

E agora temos o nosso vetor gradiente num ponto x 0 , y 0 , z 0 da superfície:

∇ F x 0 , y 0 , z 0 = - 2 x 0 , - 2 y 0 , - 1

Passo 2

Ok, e agora? A questão não só não nos deu o ponto de tangência x 0 , y 0 , z 0 do plano, como nos pediu os possíveis! Mas calma, ela disse que tanto o ponto 1,0 , 7 como o 3,0 , 3 pertencem aos planos tangentes. E o que isso significa? Então, lembra daquele vetor genérico que sempre criamos, x - x 0 , y - y 0 , z - z 0 ? As primeira coordenadas, x   e y , eram de pontos que formavam o plano, sendo que as segundas, eram do ponto de tangência, certo? Como agora temos as coordenadas x e y , de dois pontos que foram dados pelo enunciado, ainda podemos descobrir a equação do plano!

Assim, vamos montar duas equações: uma dizendo que o produto escalar entre o vetor gradiente e o vetor 1 - x 0 , 0 - y 0 , 7 - z 0 é 0 , e outra dizendo que o produto escalar entre o vetor gradiente e o vetor 3 - x 0 , 0 - y 0 , 3 - z 0 é 0 .

Então, poderemos descobrir as coordenadas dos pontos de tangência, e a equação dos dois planos!

∇ F x , y , z . 1 - x 0 , 0 - y 0 , 7 - z 0 = 0 ∇ F x , y , z . 3 - x 0 , 0 - y 0 , 3 - z 0 = 0

Passo 3

Desenvolvendo a primeira,

- 2 x 0 , - 2 y 0 , - 1 . 1 - x 0 , 0 - y 0 , 7 - z 0 = 0

- 2 x 0 + 2 x 0 . x 0 + 2 y 0 . y 0 - 7 + z 0 = 0

Desenvolvendo a segunda, temos:

- 2 x 0 , - 2 y 0 , - 1 . 3 - x 0 , 0 - y 0 , 3 - z 0 = 0

- 6 x 0 + 2 x 0 . x 0 + 2 y 0 . y 0 - 3 + z 0 = 0

Como sabemos que z = 7 - x 2 - y 2 , então:

z 0 = 7 - x 0 2 - y 0 2

E o nosso sistema fica:

- 2 x 0 + 2 x 0 2 + 2 y 0 2 - 7 + z 0 = 0 - 6 x 0 + 2 x 0 2 + 2 y 0 2 - 3 + z 0 = 0

- 2 x 0 + 2 x 0 2 + 2 y 0 2 - 7 + 7 - x 0 2 - y 0 2 = 0 - 6 x 0 + 2 x 0 2 + 2 y 0 2 - 3 + 7 - x 0 2 - y 0 2 = 0

Que vale:

2 x 0 - x 0 2 - y 0 2 = 0 6 x 0 - x 0 2 - y 0 2 = 4

Passo 4

Resolvendo o sistema

2 x 0 - x 0 2 - y 0 2 = 0 6 x 0 - x 0 2 - y 0 2 = 4

podemos subtrair a primeira equação da segunda, e teremos:

4 x 0 = 4

x 0 = 1

Colocando esse valor em qualquer uma das duas, por exemplo, na primeira, teremos:

2.1 - 1 = y 0 2

y 0 2 = 1

y 0 = ± 1

E teremos, colocando esses dois valores na equação do z 0 ,

z 0 = 7 - 1 - 1

z 0 = 5

E nossos dois pontos de tangência são 1,1 , 5 e 1 , - 1,5 !

Passo 5

Agora sim! Como sabemos em quais pontos os planos são tangentes, vamos criar dois vetores genéricos, um para cada plano, x - 1 , y - 1 , z - 5 e x - 1 , y + 1 , z - 5 .

Fazendo o produto escalar entre o vetor gradiente da superfície no primeiro ponto e o primeiro vetor genérico, teremos:

- 2.1 , - 2.1 , - 1 . x - 1 , y - 1 , z - 5 = 0

- 2 x + 2 - 2 y + 2 - z + 5 = 0

2 x + 2 y + z = 9

Fazendo o produto escalar entre o vetor gradiente e o segundo vetor genérico, teremos:

- 2.1 , - 2 . - 1 , - 1 . x - 1 , y + 1 , z - 5 = 0

- 2 x + 2 + 2 y + 2 - z + 5 = 0

2 x - 2 y + z = 9

Resposta

Planos: 2 x + 2 y + z = 9 e   2 x - 2 y + z = 9

Exercícios de Livros Relacionados

Existem pontos no hiperboloide x 2 - y 2 - z 2 = 1 nos quais o plano tangente é paralelo ao plano z = x + y ?
Em qual ponto do paraboloide y = x 2 + z 2 o plano tangente é paralelo ao plano x + 2 y + 3 z = 1 ?
Mostre que a equação do plano tangente a elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 pode ser escrita como x x 0 a 2 + y y 0 b 2 + z z 0 c 2 = 1
57 - Mostre que todo plano que é tangente ao cone z 2 = x 2 + y 2 passa pela origem.
Determine uma equação do plano tangente à superfície no ponto especificado.3 – z = x y ,( 1,1 , 1 )