Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Regra Da Cadeia Para Derivadas Parciasi De Ordem Superior

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos aprender como aplicar a regra da cadeia para derivadas parciais de ordem superior.

É… esse nome já é um pouquinho assustador, né? Mas fica tranquilo, não tem nada de muito novo não, só vai dar um pouquinho de trabalho manual mesmo.

⭐ Veja também ⭐

Derivadas Parciais de Ordem Superior

Antes de irmos direto ao ponto, vale uma breve revisão.

As derivadas parciais são usadas quando queremos derivar uma função de várias variáveis. Mais ou menos assim, para derivar a função :

A gente deriva em relação a , tratando como uma constante qualquer:

E a gente deriva em relação a , tratando como constante:

Essa aí são nossas derivadas parciais de .

Aí, se quiséssemos a segunda derivada de , teríamos que derivar cada um desses caras parcialmente mais uma vez…

Figurinha.
Figurinha.

No final de todas as contas, a gente ficaria com esse monstrinho aqui:

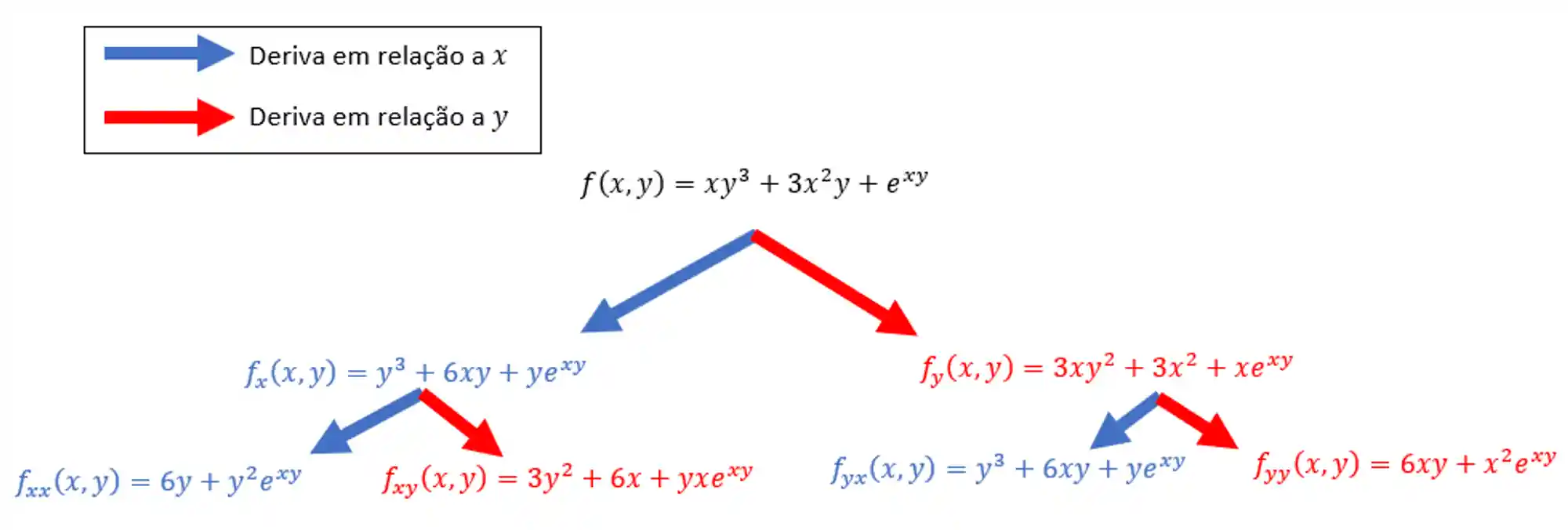
Diagrama de árvore para as derivadas parciais.
Diagrama de árvore para as derivadas parciais.

Como usar a Regra da Cadeia em Derivadas Parciais de Ordem Superior?

Agora, vamos ver como ficariam essas contas aí se a gente precisar envolver a regra da cadeia aí no meio.

Nós vamos precisar disso aqui quando nos depararmos com um função multivariável que tem suas variáveis definidas em função de outras variáveis.

Confuso demais? Vou deixar aqui um vídeo com tudo explicadinho pra você e um resuminho maravilhoso no final, caso você tenha mais facilidade assim.

Senão, segue comigo no textinho logo depois que já vai ficar tudo mais claro 😉

Se liga no exemplo 👇

Exemplo: Seja diferenciável em e e e diferenciáveis em e . Calcule .

Viu como a gente tem uma função de duas variáveis que são funções de outras variáveis? É esse tipo de caso que pede a regra da cadeia.

Pra ficar mais fácil de entender onde a gente quer chegar, vamos montar um diagrama com as ramificações parecido com o que eu fiz ali em cima.

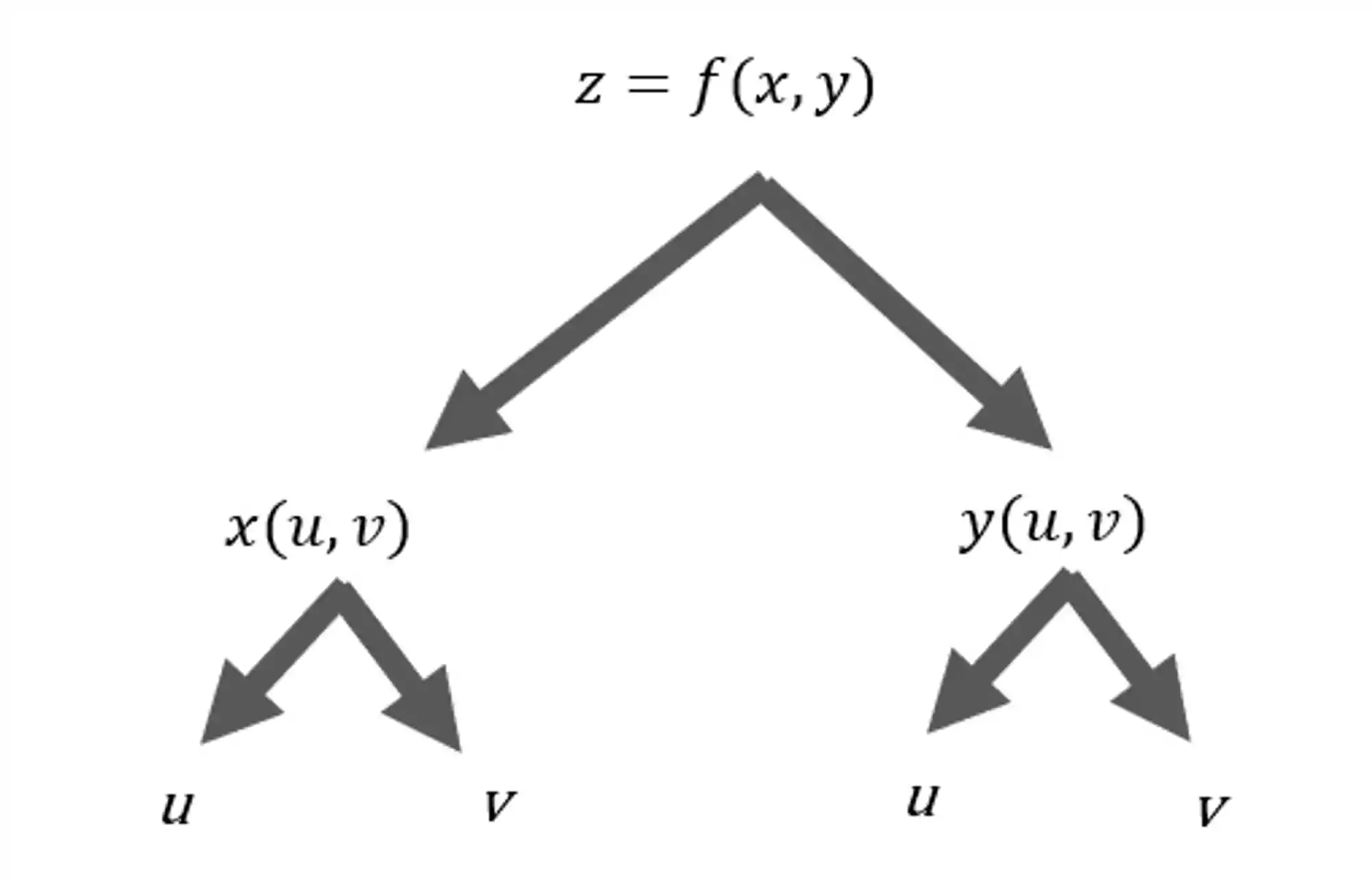
Diagrama das funções compostas.
Diagrama das funções compostas.

O que esse diagrama tá dizendo é que a gente tem a função inicial , ela é função de e , e esses caras são funções de e .

Bora adicionar a esse diagrama as derivadas parciais de cada um:

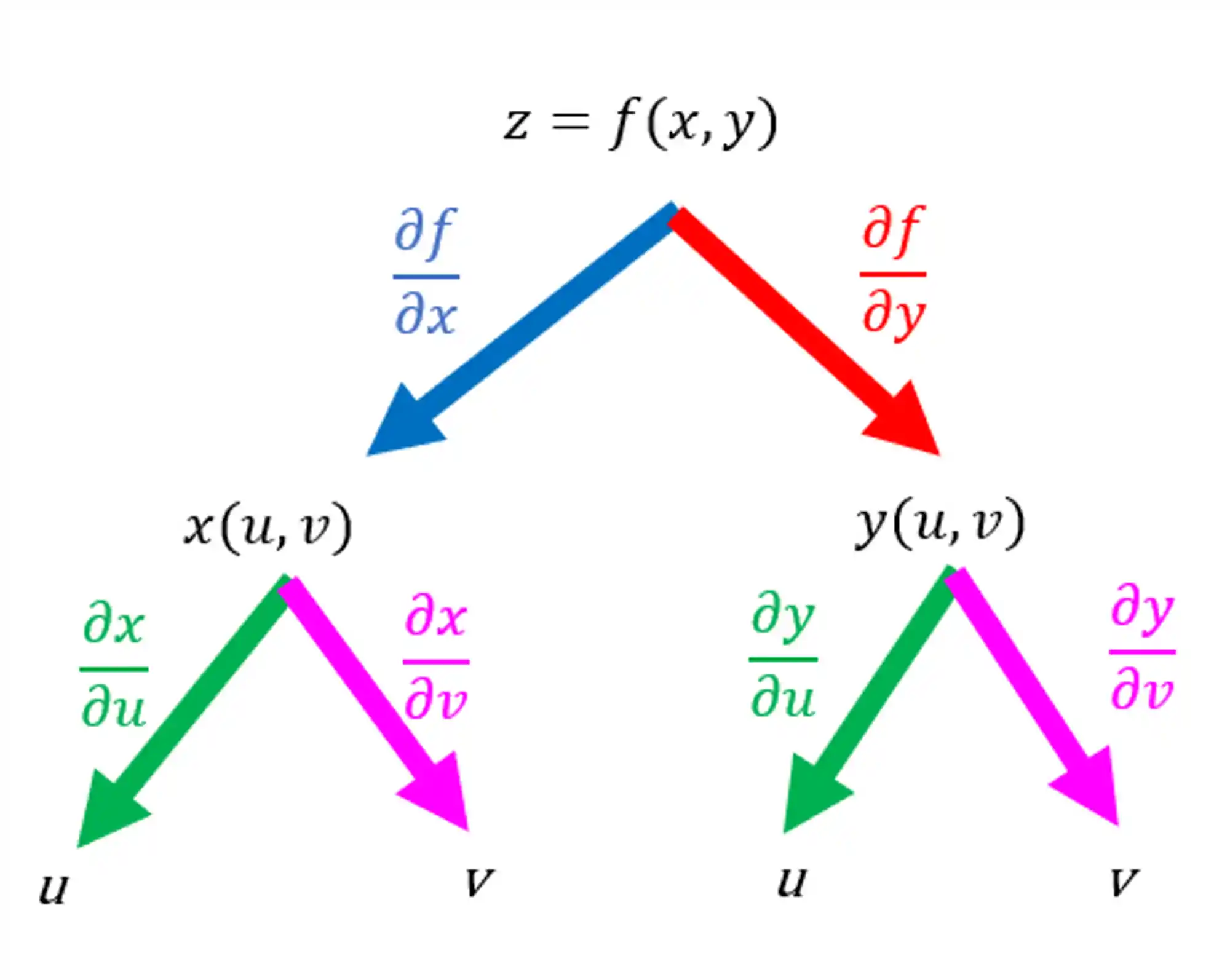
Diagrama com as derivadas parciais.
Diagrama com as derivadas parciais.

Tudo tranquilo?

O que a gente vê nesse diagrama é que a função pode ser derivada em relação a e em relação a . E as funções e podem ser derivadas em relação a e cada uma.

Agora, vamos pensar no seguinte: a gente quer chegar em , antes disso, qual caminho pelas setinhas a gente tem que percorrer pra chegar em ?

Olha, se a gente seguir por aquela setinha azul e depois pela verde:

Ilustração da regra da cadeia.
Ilustração da regra da cadeia.

Vamos ficar com

Mas ali do outro lado da árvore, a gente também pode chegar nesse resultado, concorda?

Ilustração da regra da cadeia.
Ilustração da regra da cadeia.

Aí temos:

Então, a gente precisa considerar esses dois caminhos! E fazemos isso dessa forma aqui:

Parabéns! Você acabou de deduzir a regra da cadeia para funções de várias variáveis sem nem perceber 😆

Vamos substituir uns valores nesse negócio aí? Começamos calculando cada derivada parcial que aparece nessa bagunça toda aí:

Como a gente não conhece a expressão de , deixamos do jeito que tá mesmo.

Só que tem um porém, o que a gente quer mesmo é , então a gente tem que derivar essa expressão resultante aí mais uma vez em relação a 😖

E aí o negócio começa a ficar mais complicado, por que a gente tem duas regras do produto e duas regras da cadeia. Porque todo mundo ali dentro daquele parênteses depende direta ou indiretamente de .

A partir desse ponto aqui, eu vou passar a escrever como e como , ok?

Usando a regra do produto, a gente chega nisso aqui:

Aí a gente pode ir simplificando o que a gente sabe derivar.

Agora vem a regra da cadeia. Começando por :

Substituindo os valores que a gente já conhece:

Aí repete tudo isso pra :

Agora a gente pode substituir lá naquela equação anterior:

Fazendo mais um pouquinho de contas:

Finalmente chegamos em um resultado!

Toma muito cuidado pra não errar nas continhas e não se perder no meio do caminho, beleza? Segue aquele diagrama que te mostrei que é sucesso 😉

Exemplo: Seja diferenciável em e e e diferenciáveis em e . Calcule .

Exercícios Resolvidos

Exercício Resolvido #1

Hamilton Luiz Guidorizzi, Um curso de cálculo Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, p. 286, exercício 5

Considere a função

z = ∂ f ∂ x ( x , sen ⁡ 3 x )

Verifique que

∂ z ∂ x = ∂ 2 f ∂ x 2 x , sen ⁡ 3 x + 3 cos ⁡ 3 x . ∂ 2 f ∂ y ∂ x ( x , sen ⁡ 3 x )

Passo 1

Como z já é uma derivada parcial, ∂ z ∂ x representa, na verdade, uma derivda parcial de segunda ordem de uma função composta, pois podemos dizer

x = x

y = sen ⁡ 3 x

Pela regra da cadeia, temos então:

∂ z ∂ x = ∂ ∂ x ∂ f ∂ x u , v = ∂ f x ∂ x ∂ x ∂ x + ∂ f x ∂ y ∂ y ∂ x  

Passo 2

Vamos começar pelo mais fácil:

u = x

∂ u ∂ x = 1

E

v = sen ⁡ 3 x

∂ v ∂ x = 3 cos ⁡ 3 x

Passo 3

Ok, agora ∂ f x ∂ x :

∂ f x ∂ x = ∂ 2 f ∂ x 2

E ∂ f x ∂ y :

∂ f x ∂ y = ∂ 2 f ∂ y ∂ x

Passo 4

-

Agora é só substitur tudo no ponto ( x , sen ⁡ 3 x ) e encontramos ∂ z ∂ x ( x , sen ⁡ 3 x ) :

∂ z ∂ x x , sen ⁡ 3 x = ∂ 2 f ∂ x 2 ( x , sen ⁡ 3 x )   . 1 + ∂ 2 f ∂ y ∂ x ( x , sen ⁡ 3 x )   . 3 cos ⁡ 3 x

∂ z ∂ x = ∂ 2 f ∂ x 2 ( x , sen ⁡ 3 x )   + 3 cos ⁡ 3 x ∂ 2 f ∂ y ∂ x ( x , sen ⁡ 3 x )

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

UFF, Cálculo 2B, Listas, Lista 6, questão 13

Seja g u , v = f u + v , u v , f de classe C 2 em R 2 , x = u + v , y = u v . Calcule

∂ g ∂ u 1,1   e ∂ 2 g ∂ u ∂ v 1,1

Sabendo que f x 2,1 = 3 , f y 2,1 = - 3 f x x 2,1 = 0 , f x y 2,1 = f y x 2,1 = 1 , f y y 2,1 = 2

Passo 1

Não se assuste com a cara desse maluco, vamos primeiro achar a primeira derivada em relação a u , aqui é só aplicar a regra da cadeia. Lembra que primeiro fazemos o gradiente de f

∇ f = ∂ f ∂ x , ∂ f ∂ y

Agora temos que achar esse gradiente quando u = 1 e v = 1 , primeiro vamos achar o valor de x e y

x = u + v = 1 + 1 = 2

y = u v = 1.1 = 1

Então vamos ter

∇ f 1,1 = f x 2,1 , f y 2,1 = 3 , - 3

Passo 2

Agora vamos achar a derivada da parametrização, ou seja, como a parametrização é σ u , v , vamos ter

∂ σ ∂ x = ∂ x ∂ u , ∂ y ∂ u

∂ x ∂ u = 1

∂ y ∂ u = v

Agora achamos essas derivadas no ponto u = 1 e v = 1

∂ σ ∂ x = 1,1

Passo 3

A derivada vai ficar

∂ g ∂ u = ∇ f ∙ ∂ σ ∂ x = 3 , - 3 ∙ 1,1 = 3 - 3 = 0

Passo 4

Vamos agora achar a derivada de segunda ordem, primeiro vamos reescrever o vetor gradiente para um ponto qualquer u , v

∇ f u , v = f x u + v , u v , f y u + v , u v

Agora vamos reescrever a derivada da parametrização para um ponto u , v também

∂ σ ∂ x = 1 , v

Aplicando a regra da cadeia vamos ter

∂ g ∂ u = ∇ f ∙ ∂ σ ∂ x = f x u + v , u v , f y u + v , u v ∙ 1 , v = f x u + v , u v + v f y u + v , u v

Precisamos agora derivar isso em relação a v

∂ ∂ v f x u + v , u v + v f y u + v , u v = ∂ ∂ v f x u + v , u v + ∂ ∂ v v f y u + v , u v + v ∂ ∂ v f y u + v , u v =

∂ ∂ v f x u + v , u v + f y u + v , u v + v ∂ ∂ v f y u + v , u v

Passo 5

Vamos começar achando ∂ ∂ v f x u + v , u v usando a regra da cadeia, precisamos da derivada da parametrização que já temos e o vetor gradiente de f x que vai ser

∇ f x = f x x , f x y

Aplicando em um ponto qualquer u , v

∇ f x u , v = f x x u + v , u v , f x y u + v , u v

Lembrando que

∂ σ ∂ x = 1 , v

Vamos ter

∂ ∂ v f x u + v , u v = f x x u + v , u v , f x y u + v , u v ∙ 1 , v

⇒ f x x u + v , u v + v f x y u + v , u v

Passo 6

Vamos fazer agora ∂ ∂ v f y u + v , u v usando a regra da cadeia, precisamos da derivada da parametrização que já temos e o vetor gradiente de f x que vai ser

∇ f y = f y x , f y y

Aplicando em um ponto qualquer u , v

∇ f y u , v = f y x u + v , u v , f y y u + v , u v

Lembrando que

∂ σ ∂ x = 1 , v

Vamos ter

∂ ∂ v f y u + v , u v = f y x u + v , u v , f y y u + v , u v ∙ 1 , v

⇒ f y x u + v , u v + v f y y u + v , u v

Passo 7

Vamos juntar a porra toda, vai ficar horrível mas vamos lá

∂ 2 g ∂ u ∂ v = ∂ ∂ v f x u + v , u v + f y u + v , u v + v ∂ ∂ v f y u + v , u v

⇒ f x x u + v , u v + v f x y u + v , u v + f y u + v , u v + f y x u + v , u v + v f y y u + v , u v

Precisamos agora trocar u = 1 e v = 1

f x x 1 + 1,1.1 + 1 f x y 1 + 1,1.1 + f y 1 + 1,1.1 + f y x 1 + 1,1.1 + 1 f y y 1 + 1,1.1

∂ 2 g ∂ u ∂ v 1,1 = f x x 2,1 + f x y 2,1 + f y 2,1 + f y x 2,1 + f y y 2,1

∂ 2 g ∂ u ∂ v 1,1 = 0 + 1 - 3 + 1 + 2 = 1

Resposta

∂ g ∂ u 1,1 = 0

∂ 2 g ∂ u ∂ v 1,1 = 1

Exercício Resolvido #3

UFF, Cálculo 2B, Listas, Lista 6, questão 16

Sejam z = z x , y , z de classe C 2 em R 2 , x = e u cos ⁡ v e y = e u sen ⁡ v .

Suponha que

∂ 2 z ∂ x 2 + ∂ 2 z ∂ y 2 = 0

Calcule

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2

Passo 1

Não se assuste com a cara desse maluco, vamos primeiro achar a primeira derivada em relação a u e depois a primeira derivada em relação a v . Antes de mais nada devemos fazer o gradiente de z

∇ z = ∂ z ∂ x , ∂ z ∂ y

Agora vamos achar esse gradiente para u e v

∇ z = ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v , ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

Passo 2

Calculando o gradiente de x :

x = e u cos ⁡ v

∇ x u , v = ∂ x ∂ u , ∂ x ∂ v = ( e u cos ⁡ v , - e u sen ⁡ v )

Calculando o gradiente de y :

y = e u sen ⁡ v

∇ y u , v = ∂ y ∂ u , ∂ y ∂ v = ( e u sen ⁡ v , e u cos ⁡ v )

Passo 3

Aplicando a regra da cadeia vamos ter

∂ z ∂ u = ∂ z ∂ x ∂ x ∂ u + ∂ z ∂ y ∂ y ∂ u

∂ z ∂ u = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

Passo 4

Precisamos agora derivar isso em relação a u para achar a segunda derivada disso em relação a u . Segura que lá vem regra do produto com regra da cadeia:

∂ 2 z ∂ u 2 = ∂ ∂ u e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + ∂ ∂ u e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ u 2 = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

Temos que achar aquelas derivadas separadas ali, vamos fazer isso por partes no próximo passo

Passo 5

Começando com ∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v . Isso, nada mais é que z x u .

Aplicando a regra da cadeia,

∂ ∂ u ∂ z ∂ x = z x u = ∂ z x ∂ x ∂ x ∂ u + ∂ z x ∂ y ∂ y ∂ u

Porque a derivada parcial em relação a x , z x , é uma função de x e y , mas x e y são funções de u e v , certo?

Precisamos do vetor gradiente de ∂ z ∂ x , que vai ser

∇ z x = ∂ 2 z ∂ x 2 , ∂ 2 z ∂ x ∂ y = ∂ z x ∂ x , ∂ z x ∂ y = z x x , z y x

Aplicando em um ponto qualquer

∇ ∂ z ∂ x u , v = ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v , ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v

Lembrando que

∂ x ∂ u = e u cos ⁡ v

E

∂ y ∂ u = e u sen ⁡ v

Vamos ter

∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v = ∂ z x ∂ x ∂ x ∂ u + ∂ z x ∂ y ∂ y ∂ u

∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v = e u cos ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v

Passo 6

Indo para ∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v , que é o mesmo que z y u , aplicando a regra da cadeia

∂ ∂ u ∂ z ∂ y = z y u = ∂ z y ∂ x ∂ x ∂ u + ∂ z y ∂ y ∂ y ∂ u

Precisamos do vetor gradiente de ∂ z ∂ y , que vai ser

∇ ∂ z ∂ y = ∇ z y = ∂ 2 z ∂ x ∂ y , ∂ 2 z ∂ y 2 = z y x , z y y

Aplicando em um ponto qualquer

∇ ∂ z ∂ y u , v = ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v , ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Lembrando que

∂ x ∂ u = e u cos ⁡ v

E

∂ y ∂ u = e u sen ⁡ v

Vamos ter

∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = ∂ z y ∂ x ∂ x ∂ u + ∂ z y ∂ y ∂ y ∂ u

∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = e u cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Passo 7

Vamos agora juntar essa bagunça toda,

∂ 2 z ∂ u 2 = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ u ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ u 2 = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v e u cos ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v e u cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ u 2 = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen ⁡ v cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u cos ⁡ v sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Passo 8

Ufa, parece que acabou né? Só que não

Temos que fazer a segunda derivada em relação a v agora, mas o raciocínio é todo igual a esse que usamos. Lembrando que o gradiente vai ser

∇ z = ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v , ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

E

∂ x ∂ v = , - e u sen ⁡ v

∂ y ∂ v = e u cos ⁡ v

Que calculamos lá nos passos 1 e 2.

Passo 9

Aplicando a regra da cadeia vamos ter

∂ z ∂ v = ∂ z ∂ x ∂ x ∂ v + ∂ z ∂ y ∂ y ∂ v

∂ z ∂ v = - e u sen ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

Passo 10

Precisamos agora derivar isso em relação a v para achar a segunda derivada disso em relação a v , então vamos ter, pela regra do produto e regra da cadeia:

∂ 2 z ∂ v 2 = ∂ ∂ v - e u sen ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ ∂ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + ∂ ∂ v e u cos ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ v 2 = - e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ ∂ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

Temos que achar aquelas derivadas deparadas ali, vamos fazer isso por partes no próximo passo

Passo 11

Começando com ∂ ∂ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v , que nada mais é que z x v . Aplicando a regra da cadeia

∂ ∂ v ∂ z ∂ x = z x v = ∂ z x ∂ x ∂ x ∂ v + ∂ z x ∂ y ∂ y ∂ v

Precisamos do vetor gradiente de ∂ z ∂ x , que vai ser

∇ ∂ z ∂ x = ∇ z x = ∂ 2 z ∂ x 2 , ∂ 2 z ∂ x ∂ y = z x x , z y x

Aplicando em um ponto qualquer

∇ ∂ z ∂ x u , v = ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v , ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v

Lembrando que

∂ x ∂ v = , - e u sen ⁡ v

∂ y ∂ v = e u cos ⁡ v

Vamos ter

∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = ∂ z x ∂ x ∂ x ∂ v + ∂ z x ∂ y ∂ y ∂ v

∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = - e u sen ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v

Passo 12

Indo para ∂ ∂ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v , que nada mais é que z y v . Aplicando a regra da cadeia

∂ ∂ v ∂ z ∂ y = z y v = ∂ z y ∂ x ∂ x ∂ v + ∂ z y ∂ y ∂ y ∂ v

Precisamos do vetor gradiente de ∂ z ∂ y , que vai ser

∇ ∂ z ∂ y = ∇ z y = ∂ 2 z ∂ x ∂ y , ∂ 2 z ∂ y 2 = z y x , z y y

Aplicando em um ponto qualquer

∇ ∂ z ∂ y u , v = ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v , ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Lembrando que

∂ x ∂ v = , - e u sen ⁡ v

∂ y ∂ v = e u cos ⁡ v

Vamos ter

∂ ∂ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = ∂ z y ∂ x ∂ x ∂ v + ∂ z y ∂ y ∂ y ∂ v

∂ ∂ u ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v = - e u sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Passo 13

Vamos agora juntar essa bagunça toda,

∂ 2 z ∂ v 2 = - e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ ∂ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ ∂ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ v 2 = - e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v - e u sen ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v - e u sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u cos ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ v 2 = - e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v - e 2 u cos ⁡ v sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v - e 2 u sen ⁡ v cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Passo 14

Ai ai, conta monstruosamente gigantesca, acertar uma parada dessa deveria valer uns 8 pontos numa prova, mas tudo bem, o que importa aqui é saber aplicar as derivadas e usar a regra da cadeia mil vezes, essa é uma questão que se você acompanhou tudo até o fim, não desistiu virou outra pessoa, meus parabéns por chegar até aqui eta questãozinha muito louca.

Vamos agora somar esses dois monstros que achamos

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen ⁡ v cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u cos ⁡ v sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v + - e u cos ⁡ v ∂ z ∂ x e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v 0 - e 2 u cos ⁡ v sen ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v - e u sen ⁡ v ∂ z ∂ y e u cos ⁡ v , e u sen ⁡ v - e 2 u sen ⁡ v cos ⁡ v ∂ 2 z ∂ x ∂ y e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Temos muita coisa parecida com sinal diferente aí, vamos diminuir e sumir com essa parada toda.

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u cos 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Tirando o parênteses

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u cos 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u sen 2 ⁡ v ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u cos 2 ⁡ v ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Dando uma arrumada vamos ter

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v cos 2 ⁡ v + sen 2 ⁡ v + e 2 u ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v cos 2 ⁡ v + sen 2 ⁡ v

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + e 2 u ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u ∂ 2 z ∂ x 2 e u cos ⁡ v , e u sen ⁡ v + ∂ 2 z ∂ y 2 e u cos ⁡ v , e u sen ⁡ v

Como ele disse que aquilo dentro do parêntese é 0 vamos ter

∂ 2 z ∂ u 2 + ∂ 2 z ∂ v 2 = e 2 u 0 = 0

Nesse momento deveríamos comemorar, mas se você é como eu deve estar com aquele pequeno ódio interno querendo matar alguém porque conta para cacete para dar 0 , mas ok

Resposta

0

Exercício Resolvido #4

UNICAMP, Cálculo 2m, P1 2014 Manhã, questão 2, item b

Seja h uma função de duas variáveis com derivadas se segunda ordem contínuas. Se z = h x , y , em que x = r 2 + s 2 e y = 2 r s , determine δ 2 z δ s δ r .

Passo 1

Uma simples grande e chata pra cacete aplicação da regra da cadeia! Temos uma função, que é função de duas outras, e queremos a derivada dessa função maior em relação aos argumentos das funções de dentro. A dica é imaginar como uma árvore, sendo o caule central a função principal, e nela, temos como argumentos outras funções, que vão ramificando para quantas funções quisermos até chegar nos argumentos finais.

Enfim, dei uma viajada, mas mão na massa! Derivando z x r , s , y r , s em relação a r , temos:

δ z δ r h x r , s , y r , s = δ h δ x   . δ x δ r + δ h δ y   . δ y δ r

Passo 2

Agora temos que calcular essas derivadas parciais de x e y   em relação a r :

x = r 2 + s 2

δ x δ r = 2 r

y = 2 r s

δ y δ r = 2 s

Como não sabemos que função z = h x , y é essa, vamos deixar esse nabo todo em função de h x e h y mesmo:

z r = h x . 2 r + h y   . 2 s

Passo 3

Beleza, agora temos que pegar esse z r e derivar em relação a s . É, mano, segura firme que agora é regra da cadeia mais regra do produto, essa parada vai crescer!

z r s = δ δ s h x . 2 r +   δ δ s h y . 2 s

Ou seja, para o primeiro termo, h x . 2 r , temos que derivar o h x em relação a s , multiplicar por 2 r e somar com o 2 r derivado em relação a s multiplicado por h x (é aplicar a regra do produto, derivando em relação a s ).

Fica então:

z r s = δ δ s h x . 2 r + δ δ s 2 r . h x +   δ δ s h y . 2 s + δ δ s 2 s . h y

Passo 4

Calculando a derivada em relação a s de h x , temos:

h x s = δ h x δ x . δ x δ s +   δ h x δ y . δ y δ s

Como δ x δ s e δ y δ s são:

x = r 2 + s 2

δ x δ s = 2 s

y = 2 r s

δ y δ s = 2 r

Então temos, substituindo ali em cima,

h x s = h x x . 2 s + h x y . 2 r

E não esquecendo, isso que acabamos de encontrar foi só o primeiro termo da nossa derivada de z r em relação a s ... Olha como tá ficando:

z r s = h x x . 2 s + h x y . 2 r . 2 r + δ δ s 2 r . h x +   δ δ s h y . 2 s + δ δ s 2 s . h y

Passo 5

Bom, o segundo termo, δ δ s 2 r . h x é bem simples, porque derivando em 2 r em relação a s dá 0 , pois tratamos r como constante!

Então, a derivada z r s fica:

z r s = h x x . 2 s + h x y . 2 r . 2 r + 0 +   δ δ s h y . 2 s + δ δ s 2 s . h y

Passo 6

Agora derivando h y em relação a s , teremos:

h y s = δ h y δ x   . δ x δ s + δ h y δ y   . δ y δ s

Beleza, sabemos que as derivadas δ x δ s e δ x δ s são 2 s e 2 r , respectivamente. Então,

h y s = h y x   . 2 s + h y y   . 2 r

E a nossa derivada z r s , atualizada, é:

z r s = h x x . 2 s + h x y . 2 r . 2 r +   h y x   . 2 s + h y y   . 2 r . 2 s + δ δ s 2 s . h y

Passo 7

Ufa! Só falta mais um! E esse é fácil!

Derivando 2 s em relação a s , temos 2 ! Então, por fim, nossa derivada da função z em relação a r e s é:

z r s = h x x . 2 s + h x y . 2 r . 2 r +   h y x   . 2 s + h y y   . 2 r . 2 s + 2 . h y

Fazendo as distributivas, teremos:

z r s = h x x . 4 s r + h x y . 4 r 2 + h y x   . 4 s 2 + h y y   . 4 s r + 2 . h y

Como a questão diz que as derivadas parciais de segunda ordem são contínuas, h x y = h y x , e, então, podemos colocar alguns termos em evidência:

z r s = 4 s r h x x + h y y + 4 r 2 + s 2 . h x y + 2 h y

Resposta

z r s = 4 s r h x x + h y y + 4 r 2 + s 2 . h x y + 2 h y

Exercício Resolvido #5

PUC-RJ, Cálculo 2, P2 2012.2, questão 3, item b

Seja f x , y uma função com derivadas parciais f x x . f y y , f x y = f y x contínuas. Sejam

x u , v = ln ⁡ 1 + u 2 + v 2

y u , v = e u + v sen ⁡ u v

E

g u , v = f x u , v , y u , v

Assuma que

f ln ⁡ 2 , 0 = 1 ,       f x ln ⁡ 2 , 0 = 2 ,       f y ln ⁡ 2 , 0 = e - 1

Sabendo que

f x x ln ⁡ 2 , 0 = a ,       f x y ln ⁡ 2 , 0 = b ,       f y y ln ⁡ 2 , 0 = c

Calcule g v v 0,1 em função de a , b e c .

Passo 1

Vamos começar achando o gradiente de g v , depois é só pegar a expressão e derivar de novo em relação a v .

Ele disse que

g u , v = f x u , v , y u , v

Então para acharmos a primeira derivada parcial de g , vamos usar a fórmula da regra da cadeia

g v = ∂ f ∂ x x u , v , y u , v . ∂ x ∂ v u , v + ∂ f ∂ y x u , v , y u , v . ∂ y ∂ v u , v

Fica atento aos valores que vamos usar, para f usamos   x u , v , y u , v e para x e y usamos u , v .

Passo 2

Vamos agora para g v

g v = ∂ f ∂ x x u , v , y u , v . ∂ x ∂ v u , v + ∂ f ∂ y x u , v , y u , v . ∂ y ∂ v u , v

Nós temos as funções x u , v e y u , v , vamos as derivadas

∂ x ∂ v = 1 + u 2 + v 2 ' 1 + u 2 + v 2 = 2 v 1 + u 2 + v 2

E

∂ y ∂ v = e u + v sen ⁡ u v + e u + v cos ⁡ u v ∙ u = e u + v sen ⁡ u v + e u + v u cos ⁡ u v

Para a derivada que queremos temos que achar x u , v , y u , v em u , v ,

x u , v , y u , v = ln ⁡ 1 + u 2 + v 2 , e u + v sen ⁡ u v

Temos que fazer a derivada para um u , v quaisquer para só no final substituir o valor de u , v que ele pediu.

Passo 3

Feiosinho essa parada né? Vamos derivar essa zona em relação a v , aplicando a regra da cadeia

∂ 2 g ∂ v 2 = ∂ ∂ v ∂ g ∂ v = ∂ ∂ v ∂ f ∂ x ∂ x ∂ v + ∂ f ∂ y ∂ y ∂ v

⇒ ∂ ∂ v ∂ f ∂ x ∂ x ∂ v + ∂ ∂ v ∂ f ∂ y ∂ y ∂ v

⇒ ∂ ∂ v ∂ f ∂ x ∂ x ∂ v + ∂ f ∂ x ∂ ∂ v ∂ x ∂ v + ∂ ∂ v ∂ f ∂ y ∂ y ∂ v + ∂ f ∂ y ∂ ∂ v ∂ y ∂ v

⇒ ∂ ∂ v ∂ f ∂ x ∂ x ∂ v + ∂ f ∂ x ∂ 2 x ∂ v 2 + ∂ ∂ v ∂ f ∂ y ∂ y ∂ v + ∂ f ∂ y ∂ 2 y ∂ v 2

Vamos usar a mesma ideia de antes, começando com ∂ ∂ v ∂ f ∂ x

∂ ∂ v ∂ f ∂ x = ∂ f x ∂ v = ∂ f x ∂ x ∂ x ∂ v + ∂ f x ∂ y ∂ y ∂ v = ∂ 2 f ∂ x 2 ∂ x ∂ v + ∂ 2 f ∂ x ∂ y ∂ y ∂ v

Entendeu a ideia, em vez de f colocamos ∂ f ∂ x .

Passo 4

Fazendo a mesma coisa com ∂ ∂ v ∂ f ∂ y

∂ ∂ v ∂ f ∂ y = ∂ f y ∂ v = ∂ f y ∂ x ∂ x ∂ v + ∂ f y ∂ y ∂ y ∂ v = ∂ 2 f ∂ x ∂ y ∂ x ∂ v + ∂ 2 f ∂ y 2 ∂ y ∂ v

Entendeu a ideia, em vez de f colocamos ∂ f ∂ y .

A segunda derivada de g vai ficar

∂ 2 g ∂ v 2 = ∂ 2 f ∂ x 2 ∂ x ∂ v + ∂ 2 f ∂ x ∂ y ∂ y ∂ v ∂ x ∂ v + ∂ f ∂ x ∂ 2 x ∂ v 2 + ∂ 2 f ∂ x ∂ y ∂ x ∂ v + ∂ 2 f ∂ y 2 ∂ y ∂ v ∂ y ∂ v + ∂ f ∂ y ∂ 2 y ∂ v 2

Repara que precisamos da primeira e da segunda derivada disso tudo, em relação a f é no ponto x , y , Vamos achar esses pontos

x 0,1 = ln ⁡ 1 + 0 2 + 1 2 = ln ⁡ 2

y 0,1 = e 0 + 1 sen ⁡ 0 ∙ 1 = e sen ⁡ 0 = 0

Ou seja,

x = ln ⁡ 2

y = 0

Pelo enunciado temos as derivadas de f nesses pontos, precisamos da segunda derivada de x e y em relação a v .

Passo 5

Primeiro vamos achar as primeiras derivadas de x e v no ponto 0,1

∂ x ∂ v 0,1 = 2 ∙ 1 1 + 0 2 + 1 2 = 2 1 + 1 = 2 2 = 1

∂ y ∂ v 0,1 = e 0 + 1 sen ⁡ 0 ∙ 1 + e 0 + 1 0 cos ⁡ 0 ∙ 1 = e sen ⁡ 0 = 0

Agora para as derivadas segundas.

Começando com a derivada de x

∂ 2 x ∂ v 2 = 2 1 + u 2 + v 2 - 2 v 2 v 1 + u 2 + v 2 2

∂ 2 x ∂ v 2 = 2 + 2 u 2 + 2 v 2 - 4 v 2 1 + u 2 + v 2 2

∂ 2 x ∂ v 2 = 2 + 2 u 2 - 2 v 2 1 + u 2 + v 2 2

Agora para a derivada de y

∂ 2 y ∂ v 2 = e u + v sen ⁡ u v + e u + v cos ⁡ u v ∙ u + e u + v u cos ⁡ u v + e u + v u - sen ⁡ u v ∙ u

∂ 2 y ∂ v 2 = e u + v sen ⁡ u v + e u + v u cos ⁡ u v + e u + v u cos ⁡ u v - e u + v u 2 sen ⁡ u v

Vamos agora achar essas derivadas no ponto 0,1

∂ 2 x ∂ v 2 0,1 = 2 + 2 ∙ 0 2 - 2 ∙ 1 2 1 + 0 2 + 1 2 2

∂ 2 x ∂ v 2 0,1 = 2 - 2 1 + 1 2 = 0

∂ 2 y ∂ v 2 0,1 = e 0 + 1 sen ⁡ 0 ∙ 1 + e 0 + 1 0 cos ⁡ 0 ∙ 1 + e 0 + 1 0 cos ⁡ 0 ∙ 1 - e 0 + 1 0 2 sen ⁡ 0 ∙ 1

∂ 2 y ∂ v 2 0,1 = e sen ⁡ 0 + 0 + 0 - 0 = 0

Passo 6

Voltando para a segunda derivada de g

∂ 2 g ∂ v 2 = ∂ 2 f ∂ x 2 ∂ x ∂ v + ∂ 2 f ∂ x ∂ y ∂ y ∂ v ∂ x ∂ v + ∂ f ∂ x ∂ 2 x ∂ v 2 + ∂ 2 f ∂ x ∂ y ∂ x ∂ v + ∂ 2 f ∂ y 2 ∂ y ∂ v ∂ y ∂ v + ∂ f ∂ y ∂ 2 y ∂ v 2

∂ 2 g ∂ v 2 0,1 = a ∙ 1 + b ∙ 0 ∙ 1 + 2 ∙ 0 + b ∙ 1 + c ∙ 0 0 + e - 1 ∙ 0

∂ 2 g ∂ v 2 0,1 = a ∙ 1 + 0 + b 0 + 0

∂ 2 g ∂ v 2 0,1 = a + 0 + 0 + 0

∂ 2 g ∂ v 2 0,1 = a

Resposta

∂ 2 g ∂ v 2 0,1 = a

Exercícios de Livros Relacionados

Suponha que todas as funções dadas tenham derivadas parciais de segunda ordem contínuas.Mostre que qualquer função da forma z = f x + a t + g ( x - a t ) é solução da equação de onda ∂ 2 z ∂ t 2 = a 2
Sejam z = z (x , y) , x = e^u cos ( v ) e y = e^u s e n ( v ) . Suponha que (del^2 z)/(del x^2) + (del^2 z)/(del y^2) = 0 . Calcule (del^2 z)/(del u) + (del^2 z)/(del v^2)
3. Considere a função g t = f a + h t , b + k t , com a ,b ,h e k constantes.b) Supondo f ( x , y ) de classe C 3 num aberto deR 2 , verifique que g ' ' ' t = h 3 ∂ 3 f ∂ x 3 x , y + 3 h 2 k ∂ 3 f ∂ x
8. Seja v (r , theta) = u ( x , y ) , onde x = r cos theta e y = r s e n theta . Verifique que(del^2 u)/(del x^2) + (del^2 u)/(del y^2) = (del^2 v)/(del r^2) + (1)/(r) (del v)/(del r) + (1)/(r^2) (del
5. Considere a função z = x (del f)/(del x) (2 x , x^2) . Verifique que(del z)/(del x) = (del f)/(del x) (2 x , x^3) + x [2 (del^2 f)/(del y del x) (2 x , x^2) + 3 x^2 (del^2 f)/(del x^2) (2 x , x^2)]