Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 4
A altura das ondas em mar aberto depende da velocidade do vento e do tempo durante o qual o vento se manteve naquela velocidade. Os valores da função são apresentados em pés na tabela.
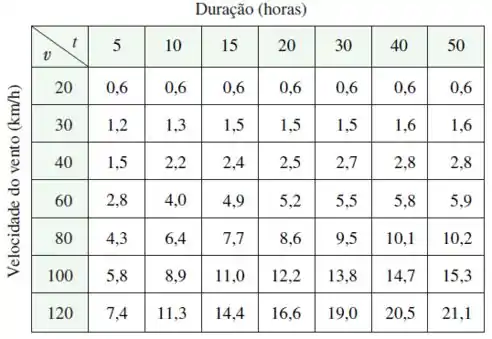
(a) Qual o significado das derivadas parciais e ?
(b) Estime os valores de e . Quais são as interpretações práticas desses valores?
(c) Qual parece ser o valor do seguinte limite?
Passo 1
Oie, meu querido amigo. Vou te ajudar a resolver essa atividade aqui.
Vamos entender a situação que nos é apresentada. Temos a tabela abaixo:
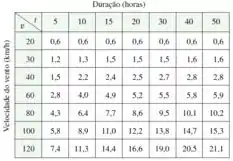
E nos é dito que essa tabela indica a altura das ondas do mar aberto, em função da velocidade do vento e do tempo em horas.
A partir disso, devemos responder o significado da derivada parcial e .
Precisaremos também estimar e que são as derivadas parciais em relação a e , para isso iremos utilizar da seguinte formula:
Essa fórmula é utilizada para calcularmos a derivada parcial de uma função em relação a . Para a derivada parcial a temos:
A última coisa que iremos fazer é analisar o limite:
Para isso, deveremos fazer algumas análises em relação a tabela e o comportamento da altura das ondas com o passar do tempo.
Passo 2
(a) Galera, a derivada parcial representa a taxa de mudança de quando fixamos e consideramos como uma função de , e ela descreve o quão rápido as alturas das ondas mudam quando a velocidade do vento muda, para uma duração de tempo fixa.
Já a derivada parcial representa a taxa de mudança de quando fixamos e consideramos como uma função de , e ela descreve o quão rápido as alturas das ondas mudam quando a duração do tempo muda, mas a velocidade do vento é constante.
(b) Para estimar vamos fixar e calcular as derivadas parciais pela definição para diferentes valores de seguindo a fórmula:
Usando e para obter as derivadas parciais nas adjacências do ponto que queremos analisar:
Fazendo uma média aritmética entre os dois valores encontrados, podemos considerar:
Isso significa que, quando um vento de sopra por horas, a altura das ondas deve crescer cerca de pés a cada de incremento na velocidade do vento, com a mesma duração de tempo.
Passo 3
Agora vamos calcular . Aqui, vamos fixar e calcular as derivadas parciais nas adjacências de pela definição:
Vamos utilizar e :
Fazendo uma média aritmética entre os dois valores encontrados, podemos considerar:
Isso significa que, quando um vento de sopra por horas, a altura das ondas deve crescer cerca de pés a cada hora de incremento na duração do tempo.
Passo 4
(c) Para valores fixos de , a função parece crescer em cada vez menores incrementos, se tornando próxima de constante à medida que cresce.
Então, a correspondente taxa de mudança se aproxima de quanto mais cresce, então parecemos ter:
Resposta
(b)
(c)