Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.5 - Ex. 10
Em cada um dos problemas de 1 a 10:
(a) Mostre que a equação diferencial dada tem um ponto singular regular em .
(b) Determine a equação indicial, a relação de recorrência e as raízes da equação indicial.
(c) Encontre a solução em série correspondente à maior raiz.
(d) Se as raízes forem diferentes e não diferirem por um inteiro, encontre também a solução em serie correspondente à menor raiz.
10.
Passo 1
a) Bom, para vemos que o primeiro termo da equação zera, isso significa que é um ponto singular, para mostrarmos que ele é regular, precisamos fazer o seguinte, reescrever a equação do jeito:
Sendo que:
E dividir tudo por :
Agora temos uma razão onde o denominador é o que está trazendo problema para a gente, vamos multiplicar a equação toda por , e aplicar o limite nessa razão:
Se o limite divergir, a singularidade é irregular, se não, é regular:
Já que o limite é finito, nosso ponto é regular.
Passo 2
b) A equação indicial, suas raízes e a equação de recorrência saem da própria equação diferencial, vamos usar então uma solução por série:
E suas derivadas:
A equação vai ficar assim:
Colocando os produtos para dentro:
A gente pode ver que tem um termo com expoente , quando , esse expoente já começa em então podemos deslocar o índice do somatório para:
E agora está tudo em termos de .
Precisamos também escrever todos os somatórios com o mesmo índice, para isso deslocamos os outros também, só que no caso deles, precisaremos expressar por fora da soma os termos que a gente desconsiderou, para manter a igualdade valida:
Passo 3
Já que a equação precisa satisfazer a igualdade, ou seja, precisa ser igual a zero para todos os , a única maneira disso ser verdade é se os coeficientes forem zero, ou seja:
Veja que, as raízes dos polinômios de no interior das duas primeiras equações são:
E:
Portanto, pra que as três equações sejam iguais a zero, a escolha de um dos coeficientes deve ser zero!
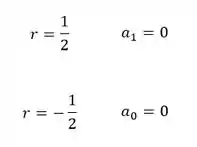
Se não as duas equações não serão simultaneamente nulas! Mas olha só a boa notícia! Como as duas raízes diferem por um inteiro, não vamos precisar fazer a letra ! Vamos considerar somente o primeiro caso, ok?
Passo 4
Agora podemos usar elas para achar a relação de recorrência. Pelo mesmo argumento que a gente usou antes, o somatório precisar satisfazer a equação, e a única maneira é se os coeficientes forem zero, então:
Isolando :
Substituindo a raiz , ficamos:
Como nesse caso, o termo e todos os coeficientes que dependerem dele, serão zero, então todos os coeficientes impares zeram. Vamos então substitui por para que possa correr todos os números ao invés de só os pares . Nossa relação fica:
Aplicando a recorrência:
Etc... Achamos então a relação:
E nossa solução é:
E ta na mão!
Resposta
- Demonstrado no passo 1