Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 23

Utilize coordenadas polares para determinar o volume do sólido dado.

Uma esfera de raio a

Passo 1

Beleza, galera? O exercício nos pede para determinarmos o volume de uma esfera de raio a .

Bom a primeira coisa que temos que entender bem É como vai ser a cara da nossa integral, como iremos usar coordenadas polares ela será assim:

V + = ∫ θ 1 θ 2   ∫ b a f ( r , θ )   r   d r   d θ

Agora fica mais fácil visualizar quem nós precisamos achar .

Para resolver essa questão precisamos encontrar quem são os intervalos de r e θ e quem será a função f ( r , θ ) .

Passo 2

Vamos começar encontrando quem é a função f ( r , θ ) .

A equação que representa a superfície de uma esfera é escrita da seguinte forma

x 2 + y 2 + z 2 = a 2

Lembrando que em coordenadas polares:

x 2 + y 2 = r 2

Utilizando coordenadas polares, podemos escrever uma integral dupla que representa o volume da metade superior de uma esfera:

x 2 + y 2 + z 2 = a 2

↓

r 2 + z 2 = a 2

z 2 = a 2 - r 2

z + = a 2 - r 2

Logo , substituindo da integral teremos

V + = ∫ θ 1 θ 2   ∫ b a a 2 - r 2   r   d r   d θ

Para calcular o volume da esfera inteira, é só multiplicar a integral por 2 :

V + = 2 ∫ θ 1 θ 2   ∫ b a a 2 - r 2   r   d r   d θ

Passo 3

Agora só precisamos encontrar os limites de integração de r e θ .

Para r nós sabemos que o seu menor valor é 0 e seu maior valor será a , que foi como representamos o raio na equação do passo 1 :

0 ≤ r ≤ a

Para achar os θ precisamos dos ângulos de uma circunferência completa:

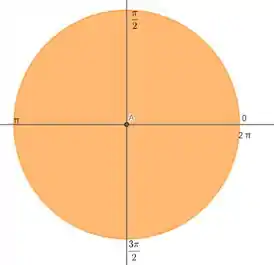
Logo:

0 ≤ θ ≤ 2 π

Substituindo na integral:

V + = 2 ∫ 0 2 π   ∫ 0 a a 2 - r 2   r   d r   d θ

Passo 4

Agora vamo calcular a integral :

Podemos separar a integral no produto de duas integrais simples:

V + = 2   ∫ 0 2 π d θ ∫ 0 a r a 2 - r 2   d r

Vamos resolver uma de cada vez e depois multiplicarmos os resultados :

⇒ ∫ 0 2 π d θ

  θ 0 2 π

2 π - 0

∫ 0 2 π d θ = 2 π

Agora vamos para a próxima:

⇒ ∫ 0 a r a 2 - r 2   d r

Para resolvermos essa integral utilizaremos o método de substituição :

u = a 2 - r 2

d x . u ' = d u

d x ( - 2 r ) = d u

d x = - d u 2 r

Substituindo na integral :

⇒ ∫ 0 a ( r u   . ) - d u 2 r

∫ 0 a ( - 1 2 u   )   d u

- 1 2 2   u 3 2 3 0 a

Substituindo u = a 2 - r 2

- a 2 - r 2 3 2 3 0 a

1 3 - a 2 - a 2 3 2 + a 2 - 0 3 2

∫ 0 a r a 2 - r 2   d r = a 3 3

Agora vamos substituir os valores que obtivemos lá na primeira integral:

V + = 2   ∫ 0 2 π d θ ∫ 0 a r a 2 - r 2   d r

↓ ↓

V + = 2   2 π a 3 3

V + = 4 π a 3 3

Resposta

4 π a 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um sistema de computação algébrico para determinar o volume exato do sólido.Delimitado por z = x 2 + y 2 e z = 2 y .
Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 - x 2 1 - xd yd x
Use um sistema de computação algébrico para determinar o volume exato do sólido.Abaixo da superfície z = x 3 y 4 + x y 2 e acima da região limitada pelas curvas y = x 3 - x e y = x 2 + x para x ≥ 0 .
Calcule ∬ D 1 - x 2 - y 2 d A , onde D é o disco x 2 + y 2 ≤ 1 , identificando primeiro a integral como o volume de um sólido.
Desenhe o sólido limitado pelo plano x + y + z = 1 e pelo paraboloide z = 4 - x 2 - y 2 e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações das fronteiras da