Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 14

Calcule a integral tripla.

∭ E x y   d V , onde E é delimitado pelo cilindro parabólico y = x 2 e x = y 2 e pelos planos z = 0 e z = x + y

Passo 1

Neste caso temos que a restrição foi dada como z entre funções das outras duas variáveis, podemos escrever a variação de z como 0 ≤ z ≤ x + y , agora as outras variáveis analisamos em uma região D do plano.

Colocando no plano y = x 2 e x = y 2

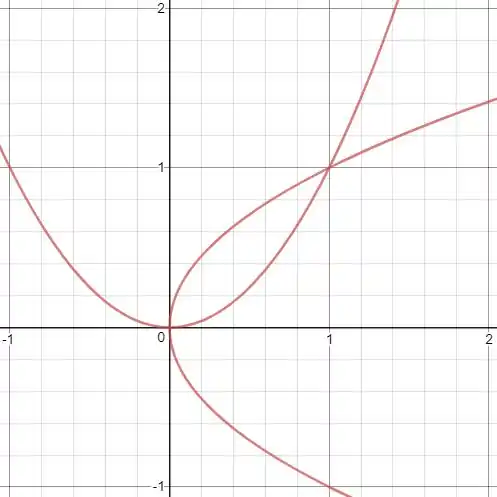
Podemos escrever D como

D = x , y 0 ≤ x ≤ 1 ,   x 2 ≤ y ≤ x }

E escrevemos E como sendo

E = x , y , z x , y ∈ D ,   0 ≤ z ≤ x + y }

Passo 2

Resolvendo a integral, temos

∭ E x y   d V = ∬ D ∫ 0 x + y x y   d z d A

∬ D x y z z = 0 z = x + y d A = ∬ D x 2 y + x y 2 d A

Agora calculando a integral dupla

∬ D x 2 y + x y 2 d A = ∫ 0 1 ∫ x 2 x x 2 y + x y 2 d y d x

= ∫ 0 1 x 2 y 2 2 + x y 3 3 y = x 2 y = x d x = ∫ 0 1 x 2 ( x ) 2 2 + x ( x ) 3 3 - x 2 x 4 2 + x . x 6 3 d x

= ∫ 0 1 x 3 2 + x 5 / 2 3 - x 6 2 - x 7 3 d x = x 4 8 + 2 x 7 / 2 21 - x 7 14 - x 8 24 0 1

= 1 8 + 2 21 - 1 14 - 1 24 = 21 + 16 - 12 - 7 168 = 18 168

= 3 28

Resposta

= 3 28

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboçar a região de integração e calcular as integrais ∫ 0 4 ∫ y 2 ∫ 0 y y d z d x d y
Esboçar a região de integração e calcular as integrais ∫ 1 2 ∫ x 2 x ∫ 0 x + y z d z d y d x
Esboçar a região de integração e calcular as integrais ∫ 1 2 ∫ 0 x 2 ∫ 0 1 x x 2 y 2 z d z d y d x
Calcule
Calcule