Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.5 - Ex. 1f
Calcule
onde é a interseção da semi-esfera com o cilindro
Passo 1
Como dito no enunciado, temos que o conjunto é a interseção entre as duas superfícies vista a baixo.
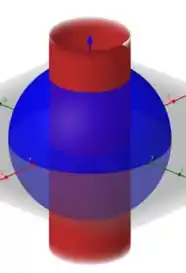
O que precisamos fazer é inicialmente buscar formas melhores de descrever nosso conjunto. Desta forma, talvez fique mais fácil de resolver nosso problema.
Passo 2
Observando de lado nosso problema, temos
Onde fazemos , e
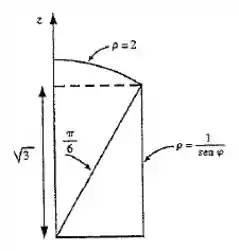
Queremos saber onde nossas superfícies se interceptam. Assim analisando a imagem a cima, temos que ela ocorre em
E pela nossa parametrização
Isso quer dizer que, seguindo a nossa parametrização, parte do nosso conjunto passa a ser nosso novo sistema de coordenada com , e A outra parte, se refere ao nosso cilindro. E segue que ele é determinado por e .
e assim nossa integral se transforma em
Onde é o jacobiano em coordenada esféricas e vale
Assim ficamos com
Passo 3
Vamos resolver as integrais separadas? Assim fica mais fácil de não se percer.
A primeira podemos já resolver em e depois e m , assim
Agora a segunda integral
Vamos fazer o mesmo, só que
Vamos correr para nossa tabelas trigonométricas. Assim temos que
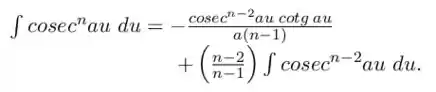
Que nos da
Que nos da
Que agora simplesmente aplicando as condições, temos