Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 2b

Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)

b) 0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 e 0 ≤ z ≤ x + y 2

Passo 1

Nesse problema iremos calcular o volume do conjunto através da integral tripla. Para isso, vamos reduzir o problema de uma integral tripla para dupla, encontrando o novo conjunto K e os intervalos de integração. Vamos lá!

Passo 2

Bom, vamos começar seguindo a sugestão de desenhar o conjunto.

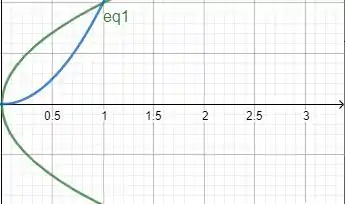
Agora, temos que o volume é dado pela integral

∫ ∫ ∫ B d x ⋅ d y ⋅ d z = ∫ ∫ K ∫ a b d z ⋅ d x ⋅ d y

Substituindo nossos intervalos, chegamos que

∫ ∫ K ∫ 0 x + y 2 d z ⋅ d x ⋅ d y = ∫ ∫ K x + y 2 ⋅ d x ⋅ d y =

Com nosso K sendo 0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 . Assim

∫ 0 1 ∫ 0 x 2 x + y 2 ⋅ d y ⋅ d x = ∫ 0 1 x ⋅ y + y 3 3 0 x 2 ⋅ d x = ∫ 0 1 x 3 + x 6 3 ⋅ d x =

= x 4 4 + x 7 21 0 1 = 1 4 + 1 21 = 21 + 4 84 = 25 84

Resposta

∫ ∫ ∫ B d x ⋅ d y ⋅ d z = 25 84

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada. ∫ 0 1 ∫ 0 z ∫ 0 y z e - y 2 d xd yd z
Calcule a integral iterada. ∫ 0 π ∫ 0 x ∫ 0 x z x 2s e nyd yd zd x
Calcule a integral iterada. ∫ 0 π / 2 ∫ 0 y ∫ 0 x cos ⁡ ( x + y + z )d zd xd y
Calcule a integral tripla. ∫ ∫ ∫ E y z cos ⁡ ( x 5 )d V , onde E = x ,y ,z0 ≤ x ≤ 1,0 ≤ y ≤ x,x ≤ z ≤ 2 x }
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y