Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.4 - Ex. 2m
Calcule o volume do conjunto dado. (Sugerimos ao leitor desenhar o conjunto.)
m) e
Passo 1
Nesse problema iremos calcular o volume do conjunto através da integral tripla. Para isso, vamos reduzir o problema de uma integral tripla para dupla, encontrando o novo conjunto e os intervalos de integração. Vamos lá!
Mas antes de prosseguimos em determinar o volume, vamos tentar entender qual é nossa figura. As equações dadas nos sugerem que estamos trabalhando com dois cilindros. Entretanto um está erguido paralelo ao plano e o segundo erquido paralelo ao plano
Que acredite, é algo um pouco complicada de se ver
Passo 2
Primeiro vamos tentar definir nossos limites de integração e depois o conjunto .
Tomando que
Assim temos
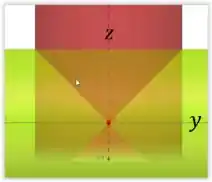
E a projeção desta interseção é a metade da circunferência no plano . Perceba que quando a gente integrar, entaremos calculando apenas do nosso volume. Isso porque as únicas partes que estamos calculando será
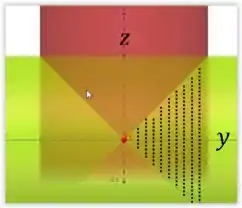
Assim não podemos esquecer do fator 4 em nossa integral
Passo 3
Temos que o volume é dado pela integral
Substituindo nossos intervalos, chegamos que
Como definimos antes, temos que a nossa projeção é a metade da circunferência podemos usar uma parametrização em coordenadas polares e ficar com
Com o jacobiano sendo . Substituindo na integral e resolvendo, chegamos que
Integrando em
E a integral de seno é o menos cosseno, ou seja