Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.5 - Ex. 14

Considere o problema de valor inicial

y ' ' + γ y ' + y = δ ( t - 1 ) ,   y ( 0 ) = 0 ,   y ' ( 0 ) = 0 ,

em que γ é o coeficiente de amortecimento (ou resistência).

  1. Seja γ = 1 2 . Encontre a solução do problema de valor inicial e desenhe seu gráfico.
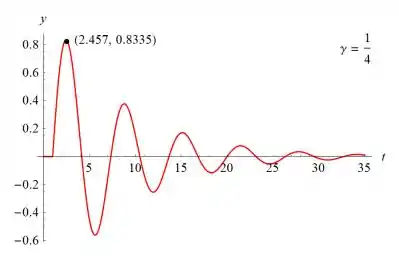
  2. Encontre o instante t 1 no qual a solução atinge seu valor máximo. Encontre, também, esse valor máximo y 1 da solução.
  3. Seja γ = e repita os itens (a) e (b).
  4. Determine como t 1 e y 1 variam quando γ diminui. Quais são os valores de t 1 e de y 1 quando γ = 0?

Passo 1

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   ℒ { y ( t ) } = ∫ 0 ∞ e - s t y ( t )   d t

Consequentemente, as derivadas se transformam da seguinte maneira.

ℒ { d y d t } = s Y ( s ) - y ( 0 )

ℒ { d 2 y d t 2 } = s 2 Y ( s ) - s y ( 0 ) - y ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

ℒ { y ' ' + γ y ' + y   } = ℒ { δ ( t - 1 ) }

ℒ { y ' ' } + γ ℒ { y ' } + ℒ { y } = ℒ { δ ( t - 1 ) }

[ s 2 Y ( s ) - s y ( 0 ) - y ' ( 0 ) ] + γ [ s Y ( s ) - y ( 0 ) ] + Y ( s ) = ∫ 0 ∞ e - s t δ ( t - 1 ) d t

Passo 2

Aplique as condições iniciais y ( 0 ) = 0 ,   y ' ( 0 ) = 0 .

s 2 Y ( s ) + γ s Y ( s ) + Y ( s ) = e - s

( s 2 + γ s + 1 ) Y ( s ) = e - s

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

Y ( s ) = 1 s ² + γ s + 1 e - s

Passo 3

Agora, basta resolver esta equação e achar sua inversa, chegando em:

y ( t ) = ℒ - 1 { Y ( s ) } = 1 2 [ s e n h ( t - 1 ) - s e n ( t - 1 ) ] u 1 ( t )

Passo 4

Suponha que 0

Y ( s ) = 2 4 - γ 2 4 - γ 2 2 ( s + γ 2 ) 2 + 4 - γ 2 4 e - s

Faça a conversão inversa de Laplace para obter y (t).

y ( t ) = 2 4 - γ ² e - γ ( t - 1 ) 2 s e n [ 4 - γ ² 2 ( t - 1 ) ] H ( t - 1 )

Para valores de t> 1, a função Heaviside é 1.

y ( t ) = 2 4 - γ 2 e - γ ( t - 1 ) 2 s e n [ 4 - γ ² 2 ( t - 1 ) ] ,   t   > 1 .

Pegue a derivada e defina-a igual a zero para encontrar o valor de t para o qual y (t) é máximo.

y ' ( t ) = - γ 4 - γ ² e - γ ( t - 1 ) / 2   s e n [ 4 - γ 2 2 ( t - 1 ) ] + k e - γ ( t - 1 ) / 2 c o s [ 4 - γ ² 2 ( t - 1 ) ] = 0

t 1 = 1 + 2 4 - γ 2 t a n - 1 ( 4 - γ ² γ )

Agora, conecte esse valor de t em y (t) para encontrar o valor máximo de y.

y ( t 1 ) = y 1 = 2 k 4 - γ 2 e x p [ - γ 4 - γ 2 t a n - 1 ( 4 - γ 2 γ ) ] s e n ( t a n - 1 ( 4 - γ 2 γ ) )

Para determinar o seno da tangente inversa, desenhe o triângulo direito implícito

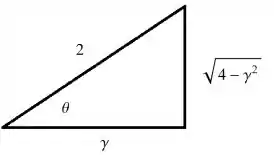
Vemos que já que o seno é 4 - γ 2 / 2 .

y 1 = e x p [ - γ 4 - γ 2 t a n - 1 ( 4 - γ 2 γ ) ]

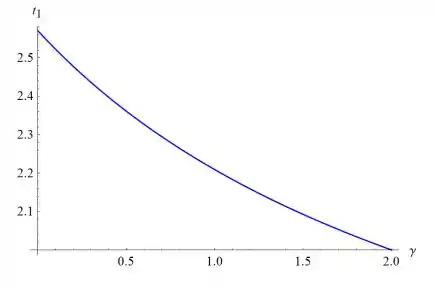
Abaixo estão os gráficos de t1 versus γ e y1 versus γ.

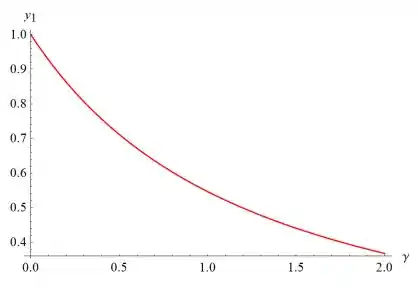
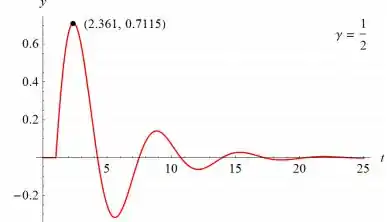
Em particular, se γ = 1/2, então

y ( t ) = 4 15 e - ( t - 1 ) / 4 s e n ( 15 4 ( t - 1 ) ) H ( t - 1 )

t 1 = 1 + 4 15 t a n - 1 15 = 2.361

y 1 = e x p ( - 1 15 t a n - 1 15 ) = 0.7115

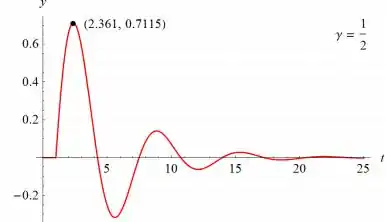
e se γ = 1/4, então

y ( t ) = 8 63 e - ( t - 1 ) / 8 s e n ( 63 8 ( t - 1 )   )   H ( t - 1 )

t 1 = 1 + 8 63 t a n - 1 63 = 2.457

y 1 = e x p ( - 1 63 t a n - 1 63 ) = 0.8335

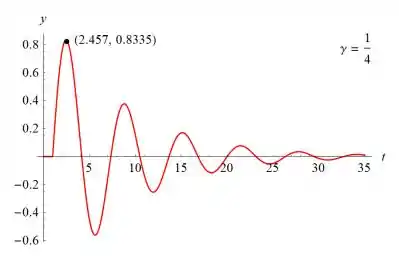
Resposta

  1. y ( t ) = ℒ - 1 { Y ( s ) } = 1 2 [ s e n h ( t - 1 ) - s e n ( t - 1 ) ] u 1 ( t )
  2. t 1 = 1 + 4 15 t a n - 1 15 = 2.361

    3. y 1 = e x p ( - 1 15 t a n - 1 15 ) = 0.7115

  3. t 1 = 1 + 8 63 t a n - 1 63 = 2.457

    4. y 1 = e x p ( - 1 63 t a n - 1 63 ) = 0.8335

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As transformações de Laplace de certas funções podem ser encontradas de modo conveniente pelas suas expansões em séries de Taylor.Use a série de Taylor para sen ⁡ t : sen ⁡ t = ∑ n = 0 ∞ - 1 n t 2 n +
a)Use o método de variação dos parâmetros para mostrar que a solução do problema de valorinicial y ″+2 y '+2 y=f( t ) ;y ( 0 )= 0 ,y '( 0 )=0 É y = ∫ 0 t e - t - τ f τ s e n t - τ d τ (b) Mostre que,
Os problemas de 17 a 22 tratam do efeito de uma sequência de impulsos aplicados em um oscilador não amortecido. Suponha que y ″+y=f( t ) ,y ( 0 )=0 ,y '( 0 )=0 . Para cada uma das escolhas para f ( t
a)Use o método de variação dos parâmetros para mostrar que a solução do problema de valorinicial y ″+2 y '+2 y=f( t ) ;y ( 0 )= 0 ,y '( 0 )=0 É y = ∫ 0 t e - t - τ f τ s e n t - τ d τ (b) Mostre que,
Proceda como no Problema 23 para o oscilador satisfazendo y ' ' + 0,1 y ' + y = ∑ k = 1 15 δ t - 2 k - 1 π ,y 0 = 0 , y ' 0 = 0 . Note que, exceto pelo termo de amortecimento, esse problema é igual ao