Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 22

Considere o problema de valor inicial

y ' ' + 0.1 y ' + y = g ( t ) ,             y ( 0 ) = 0 ,   y ' ( 0 ) = 0 ,

em que g(t) é a mesma que no Problema 21.

  1. Desenhe o gráfico da solução. Use um valor de n suficientemente grande e um intervalo de tempo longo o bastante para que a parte transiente da solução torne-se desprezível e o estado estacionário apareça claramente.
  2. Estime a amplitude e a frequência da parte correspondente ao estado estacionário da solução.
  3. Compare os resultados do item (b) com os do Problema 20 e os da Seção 3.8 para um oscilador sob a ação de uma força senoidal.

Passo 1

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   ℒ { y ( t ) } = ∫ 0 ∞ e - s t y ( t )   d t

Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.

ℒ { d y d t } = s Y ( s )   -   y ( 0 )

ℒ { d ² y d t ² } = s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

ℒ { y ' ' + 0.1 y ' + y } = ℒ { u 0 ( t ) + ∑ k = 1 n ( - 1 ) k u k π ( t ) }

[ s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 ) ] + 0.1 [ s Y ( s )   -   y ( 0 ) ] + Y ( s ) =

= ∫ 0 ∞ e - s t u 0 ( t ) d t   + ∑ k = 1 n ( - 1 ) k ∫ 0 ∞ e - s t u 0 ( t ) d t   + ∑ k = 1 n ( - 1 ) k ∫ 0 ∞ e - s t u k π ( t ) d t

Passo 2

Aplique as condições iniciais, y ( 0 ) = 0 e y ' ( 0 ) = 0 .

( s ² + 1 10 s + 1 ) Y ( s ) = 1 s + ∑ k = 1 n ( - 1 ) k ( e - k π s s )

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

Y ( s ) = [ 1 s - s + 1 20 ( s + 1 20 ) 2 + 399 400 - 1 399 399 20 ( s + 1 20 ) 2 + 399 400 ] + ∑ k = 1 n ( - 1 ) k [ 1 s - s + 1 20 ( s + 1 20 ) 2 + 399 400 - 1 399 399 20 ( s + 1 20 ) 2 + 399 400 ] e - k π s

Passo 3

Agora, basta resolver esta equação e achar sua inversa, chegando em:

y ( t ) = ℒ - 1 { Y ( s ) } = 1 - e - t / 20 c o s ( 399 20 t ) - 1 399 e - t / 20 s e n ( 399 20 t )

+ ∑ k = 1 n ( - 1 ) k { 1 - e - ( t - k π ) / 20 c o s [ 399 20 ( t - k π ) ] - 1 399 e - ( t - k π ) / 20 s e n [ 399 20 ( t - k π ) ] } H ( t - k π )

Passo 4

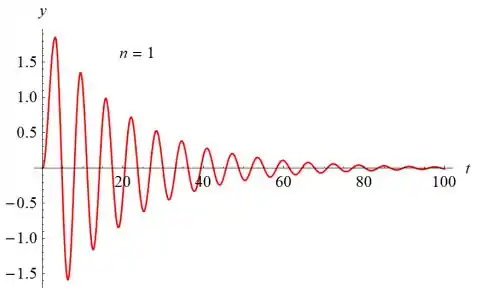
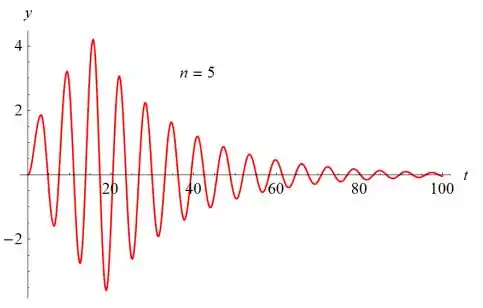
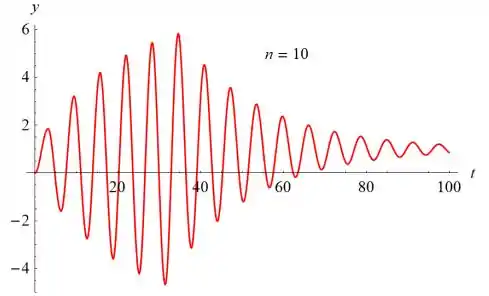
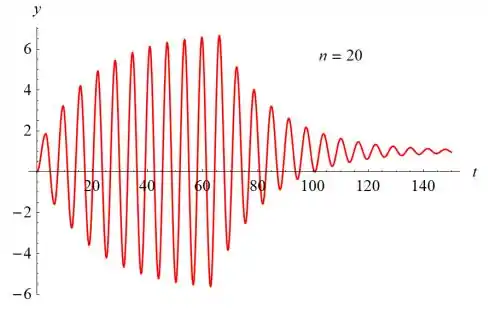
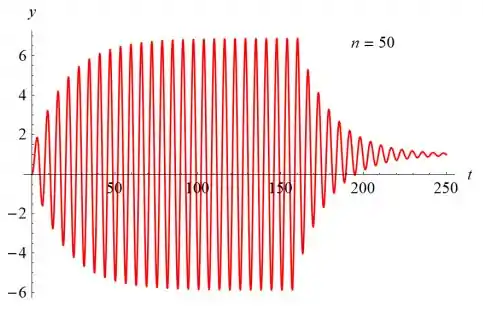
A amplitude da parte estável da solução é de cerca de 12,6 e o período é T = 2 π , o que significa que a frequência angular é ω = 2 π / T = 1 . O problema correspondente com um termo de força senoidal foi considerado na Seção 3.8.

Passo 5

z ' ' + 0.1 z ' + z = 1 + c o s ( t ) ,   z ( 0 ) = 0 ,   z ' ( 0 ) = 0 .

A solução para essa EDO é:

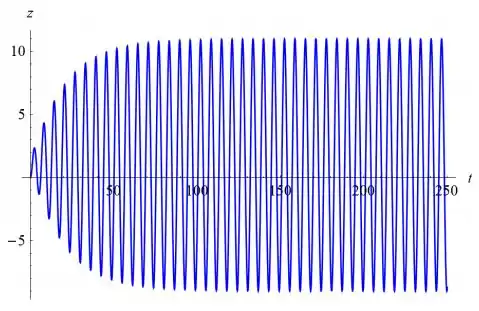
A amplitude da parte estável da solução aqui é de cerca de 9,9, e o período é T = 2 π o que significa que a frequência angular é ω = 2 π / T = 1 . Essa diferença de amplitude se deve ao fato de que a força do cosseno varia em força com o tempo, enquanto f(t) fornece pulsos com força máxima.

Resposta

  1. y ( t ) = ℒ - 1 { Y ( s ) } = 1 - e - t / 20 c o s ( 399 20 t ) - 1 399 e - t / 20 s e n ( 399 20 t ) + ∑ k = 1 n ( - 1 ) k { 1 - e - ( t - k π ) / 20 c o s [ 399 20 ( t - k π ) ] - 1 399 e - ( t - k π ) / 20 s e n [ 399 20 ( t - k π ) ] } H ( t - k π )
  2. T = 2 π , ω = 2 π / T = 1 .
  3. A amplitude da parte estável da solução aqui é de cerca de 9,9, e o período é T = 2 π o que significa que a frequência angular é ω = 2 π / T = 1 . Essa diferença de amplitude se deve ao fato de que a força do cosseno varia em força com o tempo, enquanto f(t) fornece pulsos com força máxima.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 4 y = 2 δ ( t - π / 4 ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 0 .
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + y = u π / 2 ( t ) + 3 δ ( t - 3 π / 2 ) - u 2 π ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 0 .
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 4 y = δ ( t - 4 π ) ;y ( 0 ) = 1 2 , y ' ( 0 ) = 0 .
Considere o problema de valor inicial y ' ' + γ y ' + y = δ ( t - 1 ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 , em que γ é o coeficiente de amortecimento (ou resistência).Seja γ = 1 2 . Encontre a solução do prob
Encontre a solução do problema de valor inicial dado.Desenhe um gráfico da solução. y ' ' + 3 y ' + 2 y = δ ( t - 5 ) + u 10 ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 1 2