Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 5

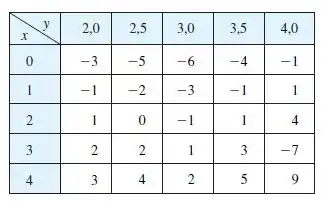
É dada a tabela de valores de uma função f   ( x ,   y ) definida em R = 0,4 × [ 2,4 ] .

(a) Estime ∬ R f ( x , y ) d A utilizando a Regra do Ponto Médio com m = n = 2 .

m = n = 4 , escolhendo como pontos de amostragem os pontos mais próximos da origem.

Passo 1

E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!

(a) O problema pede para usarmos a regra do ponto médio. Devemos aplicar essa fórmula aqui oh:

∬ R f ( x , y ) d A ≈ ∑ i = 1 2 ∑ j = 1 2 f x - , y - Δ A

Neste caso, m e n representam o número de subintervalos em que dividimos os intervalos x e y , respectivamente. Esses valores determinam quantos pontos médios serão escolhidos em cada direção para a estimativa da integral dupla.

No caso da Regra do Ponto Médio, ao escolher m = n = 2 , estamos dividindo os intervalos x e y em 2 subintervalos cada. Isso significa que teremos um total de 2   x   2 = 4 sub-retângulos formados na região R .

Portanto, ao aplicar a fórmula da Regra do Ponto Médio, calcularemos a soma dos valores da função nos pontos médios desses 4 sub-retângulos, multiplicados pela área de cada um deles.

O desenho abaixo mostra os intervalos em x e em y e com as divisões em dois espaços:

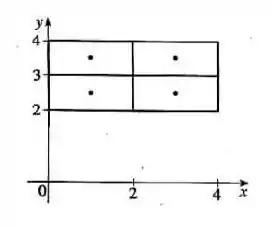
Os pontos médios vão ser:

1 ; 2,5 ; 1 ; 3,5 ; 3 ; 2,5 e   ( 3 ; 3,5 )

Daí aplicando esses pontos na fórmula teremos:

∑ i = 1 2 ∑ j = 1 2 f x - , y - Δ A = f 1 ; 2,5 Δ A + f 1 ; 3,5 Δ A + f 3 ; 2,5 Δ A + f 3 ; 3,5 Δ A

E o Δ A ? É o valor da área dos retângulos. Como dividimos o intervalo em 2 , a base vai ser 1 e a altura 2 , daí a área vai ser: Δ A = 2.1 = 2

Passo 2

Pronto! Agora é só aplicar na fórmula! Bora lá? Consultando os valores da tabela temos o seguinte:

∑ i = 1 2 ∑ j = 1 2 f x - , y - Δ A = 2 - 2 - 1 + 2 + 3 = 4

Passo 3

(b) Agora queremos estimar a integral dupla fazendo a divisão em 4 espaços iguais e pegando os pontos mais próximos à origem, ou seja, os cantos inferiores esquerdos. Vamos fazer um desenho desses retângulos pra ver melhor quais são esses pontos:

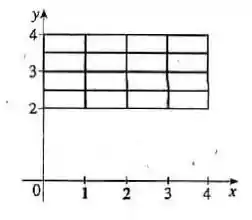Os pontos dos cantos inferiores esquerdos são:

0,2 ; 0 ; 2,5 ; 0,3 ; ( 0 ; 3,5 )

1,2 ; 1 ; 2,5 ; 1,3 ; ( 1 ; 3,5 )

2,2 ; 2 ; 2,5 ; 2,3 ; ( 2 ; 3,5 )

3,2 ; 3 ; 2,5 ; 3,3 ; ( 3 ; 3,5 )

E o valor de Δ A vai ser diferente. A base é 1 , mas a altura é 1 / 2 então a área é:

Δ A = 1 . 1 2 = 1 2  

Passo 4

Agora que temos todos os pontos e valor de Δ A , precisamos aplicar na fórmula e consultar na tabela os valores:

∬ R f ( x , y ) d A ≈ ∑ i = 1 4 ∑ j = 1 4 f x , y Δ A = f 0,2 Δ A + f 0 ; 2,5 Δ A + f 0,3 Δ A + f 0 ; 3,5 Δ A + f 1,2 Δ A + f 1 ; 2,5 Δ A + f 1,3 Δ A + f 1 ; 3,5 Δ A + f 2,2 Δ A + f 2 ; 2,5 Δ A + f 2,3 Δ A + f 2 ; 3,5 Δ A + f 3,2 Δ A + f 3 ; 2,5 Δ A + f 3,3 Δ A + f 3 ; 3,5 Δ A

E consultando os valores na tabela teremos a estimativa, saca só:

1 2 - 3 - 5 - 6 - 4 - 1 - 2 - 3 - 1 + 1 + 0 - 1 + 1 + 2 + 2 + 1 + 3 = - 8

Resposta

a ) 4

b ) - 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla. ∬ R y e - x y d A ; R = 0,2 × [ 0,3 ]
Calcule a integral dupla. ∬ R 1 1 + x + y d A ; R = 1,3 × [ 1,2 ]
Calcule a integral dupla.29. ∬ R x y 2 x 2 + 1 d A , R = x , y 0 ≤ x ≤ 1 ; - 3 ≤ y ≤ 3 }
Calcule a integral dupla.∬_R (y + x y^(- 2)) d A ; R = {(x , y)| 0 = x = 2 ; 1 = y = 2 }
Use simetria para calcular a integral dupla. ∬ R x y 1 + x 4 d A ; R = x , y - 1 ≤ x ≤ 1 ; 0 ≤ y ≤ 1 }