Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.6 - Ex. 1

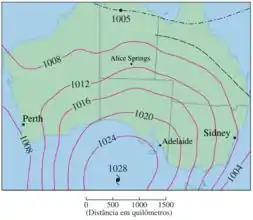
É dado o mapa de contornos mostrando a pressão barométrica em hectopascais (hPa) na Austrália em 28 de dezembro de 2004. Estime o valor da derivada direcional da função pressão em Alice Springs na direção de Adelaide. Quais são as unidades da derivada direcional?

Passo 1

Oie, tudo bem meu amigo? Vou te ajudar a resolver essa atividade hoje.

Aqui a gente tem o mapa de contorno mostrando a pressão na Australia em 28 de dezembro de 2004 :

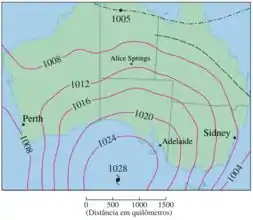
Eles nos pedem então para que criemos uma estimativa da derivada direcional da função da pressão partindo de Alice Springs para Adelaide.

Podemos aproximar a derivada direcional da função pressão em Alice na direção de Adelaide pela taxa média de mudança de pressão entre os pontos onde a linha vermelha cruza as curvas de nível mais próximas de Alice (estender a linha vermelha ligeiramente à esquerda).

Passo 2

Analisando o mapa temos:

Pressão barométrica em Adelaide

≅ 1023 h P a

Pressão barométrica em Alice Spring

≅ 1010 h P a

Pelo mapa, a distância entre as duas cidades é de 2,5   c m aproximadamente. Pela escala dada embaixo do mapa, temos:

2,2 c m – 1500 k m

2,5 c m – x

Fazendo essa regra de 3 :

x = 1704 . 55   k m

A derivada direcional da pressão pode ser encontrada a partir do seguinte cálculo:

D u P = 1023 - 1010 1704 . 55

D u P = 0 . 008   h P a

Resposta

0,008   h P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4-6. Determine a derivada direcional def no ponto dado e na direção indicada pelo ângulo θ .5. f x ,y = y cos ⁡ x y ,0 ,1 ,θ = π 4
7-10.a) Determine o gradiente de f .b) Calcule o gradiente no ponto P .c) Determine a taxa de variação de f em P na direção do vetor u .10. f x ,y ,z = y 2 e x y z ,P 0 ,1 ,- 1 ,u = 3 13 , 4 13 , 12 1
19 - Encontre a derivada direcional de f x , y = x y no ponto P ( 2,8 ) na direção do ponto Q ( 5,4 ) .
14.1. O mapa de contorno mostra a precipitação média de neve (em polegadas) perto do Lago Michigan. Estime o valor da derivada direcional da função da precipitação de neve em Muskegon, Michigan, na di
Nos exercícios de 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados. 3 )f x ,y , z = x y + z , P 2 ,1 ,0n ad i r e ç ã od oe i x op o s i t i v od o sz . çã