Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 15

Defina as integrais iteradas para ambas as ordens de integração. Então, calcule a integral dupla usando a ordem mais fácil e explique por que ela é mais fácil

∬ D y d A

D é limitada por y = x - 2 , x = y 2 .

Passo 1

E aí pessoal! Hoje vamos encarar um problema interessante de integração em uma região geral. Precisamos definir a nossa região D como sendo do tipo I e do tipo II. Vamos relembrar os conceitos básicos:

  • Região do Tipo l: Limitada acima e abaixo por curvas, e lateralmente por retas verticais. O domínio é:

    • D = x , y x 0 ≤ x ≤ x 1 ,   g x ≤ y ≤ f x }

  • Região do Tipo ll: Limitada lateralmente por curvas, e acima e abaixo por retas horizontais. O domínio é:

D = x , y y 0 ≤ y ≤ y 1 ,   g y ≤ x ≤ f y }

Vamos começar por esboçar o gráfico da nossa região. Posteriormente, vamos escrever cada uma das regiões.

Passo 2

Primeiramente, vamos esboçar a nossa região. Portanto,

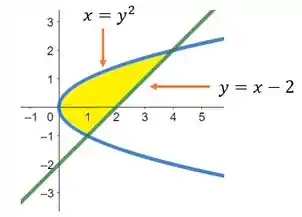
As duas curvas se intersectam nos pontos em que:

x r e t a = x p a r á b o l a

y 2 = y + 2

y 2 - y - 2 = 0

y - 2 ⋅ ( y + 1 ) = 0

Portanto, no ponto A = ( 1 , - 1 ) e no ponto B = 4,2 .

Passo 3

Agora podemos começar a escrever a nossa região D .

Como a região do tipo I é limitada acima por uma curva e abaixo por outra, temos um problema para a nossa região. Isto decorre do fato de termos 2 curvas distintas na parte inferior da região!

Por causa disto, precisamos separar a nossa região D em duas partes, uma parte à esquerda de x = 1 e outra à direita de x = 1 , pois este é o ponto em que há uma mudança na parte inferior da região.

Portanto, seja D 1 a região à esquerda, temos:

- x ≤ y ≤ x

Já os limites laterais são: 0 ≤ x ≤ 1 . Já para a região à direita, temos:

x - 2 ≤ y ≤ x

E os limites laterais são: 1 ≤ x ≤ 4 . Portanto, a nossa integral é:

∬ D y d A = ∫ 0 1 ∫ - x x y d y d x + ∫ 1 4 ∫ x - 2 x y d y d x

Passo 4

Vamos escrever agora a nossa região como uma região do tipo II. Como ela é limitada a esquerda apenas por uma curva e a direita apenas por outra curva, podemos definir esta região como um todo. Portanto, temos:

y 2 ≤ x ≤ y + 2

Acima ela é limitada pela reta y = 2 (se resume a um ponto) e abaixo por outra reta y = - 1 . Observem que estas retas são dadas pelos pontos de interseção das curvas. Portanto, a nossa integral é:

∬ D y d A = ∫ - 1 2 ∫ y 2 y + 2 y d x d y

Passo 5

A forma mais fácil de resolver esta integral é a partir da região do tipo II, pois conseguimos descrever em função de apenas uma integral. Portanto, resolvendo-a,

∬ D y d A = ∫ - 1 2 ∫ y 2 y + 2 y d x d y

∫ - 1 2 y x y 2 y + 2 d y = ∫ - 1 2 y ( y + 2 - y 2 ) d y

∫ - 1 2 ( - y 3 + y 2 + 2 y ) d y = - y 4 4 + y 3 3 + y 2 - 1 2

- 4 + 8 3 + 4 - - 1 4 - 1 3 + 1 = 8 3 - 5 12

∫ - 1 2 ∫ y 2 y + 2 y d x d y = 27 12 = 9 4

Resposta

∫ - 1 2 ∫ y 2 y + 2 y d x d y = 9 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No cálculo de uma integral dupla sobre uma região D , obtivemos uma soma de integrais iteradas como a que segue: ∬ D f x , yd A = ∫ 0 1 ∫ 0 2 y f x , yd xd y + ∫ 1 3 ∫ 0 3 - y f x , yd xd y Esboce a r
Use a geometria ou simetria, ou ambas, para calcular a integral dupla ∬ D 2 x + 3 y d A D é o retângulo 0 ≤ x ≤ a , 0 ≤ y ≤ b
Desenhe um exemplo de uma região que seja Tanto do tipo I quanto do tipo II;Nem do tipo I nem do tipo II.
Desenhe um exemplo de uma região que seja Do tipo I, mas não do tipo IIDo tipo II, mas não do tipo I
Esboce a região de integração e mude a ordem de integração. ∫ 0 2 ∫ x 2 4 f x , y d y d x