Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 12a
12. Descreva o domínio e as superfícies de nível das funções abaixo.
a)
Passo 1
Vamos começar descrevendo o domínio de .Como essa função é uma função racional, o único problema de definição que pode ocorrer é se o denominador for . Dado isso, a única restrição no domínio é: .
Então temos que nosso domínio é:
Agora para esboçar as superfícies de nível, vamos lembrar o que são. Uma superfície de nível é o conjunto dos pontos:
Esse tipo de superfície são esferas centradas em e de raio . Sendo assim, as superfícies de nível são da seguinte forma:
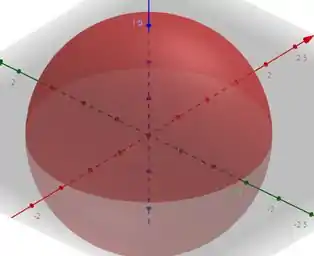
Resposta
Análise acima.
Exercícios de Livros Relacionados
Desenhar as curvas de nível C k para os valores dek dados.a) z = x 2 - y 2 ; k = 0,1 , 2,3
Dada a função f x , y = x + y 2 x + y :a)Dar o domínio;b)Calcular f ( x + ∆ x , y ) ;c)calcular f ( - 1,0 ) ;d) Fazer um esboço do gráfico do domínio.
A partir da equação dada, definir duas funções de duas variáveis, determinando seu domínio.b) x 2 + y - 3 2 + z 2 = 9
Desenhar as curvas de nível C k para os valores dek dados.b) z = y 2 - x 2 ; k = 0,1 , 2,3
Desenhar as curvas de nível C k para os valores dek dados.c) z = 2 - x 2 + y 2 ; k = - 3 , - 2 , - 1,0 , 1,2