Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.2 - Ex. 34
Desenhe o sólido contido entre as superfícies e para . Utilize um sistema de computação algébrica para aproximar o volume desse sólido até a quarta casa decimal.
Passo 1
Beleza, galera? Pra ter uma ideia de como é o sólido descrito no enunciado, vamos desenhar as superfícies e no quadrado :
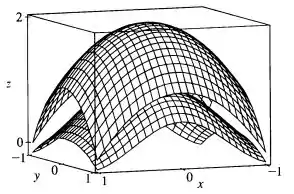
Passo 2
Show! Pra conseguirmos fazer uma estimativa do volume do sólido, primeiro precisamos escrever uma integral dupla que o represente:
Assim, utilizando um SCA, aproximamos o valor do volume:
Resposta
Exercícios de Livros Relacionados
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a :h) 1 x + y 2
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a : b )x - y
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:m) 1 1 + x 2 + 2 x y + y 2
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:l) x s e n( π y )
Seja A o retângulo 1 ≤ x ≤ 2 , 0 ≤ y ≤ 1 . Calcule ∬ A f x , y d x d y , sendo f x , y igual a:j) x y 2