Desenhe a superfície de nível correspondente a
a)
Passo 1
Perceba que nossa superfície de nível nos fornece a equação de uma elipsóide, pois há um que multiplica . Então agora é só desenhar, parça!
Resposta
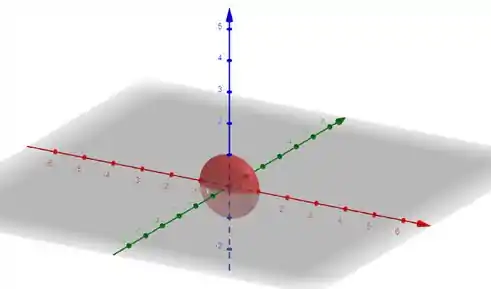
Desenhe a superfície de nível correspondente a
a)
Perceba que nossa superfície de nível nos fornece a equação de uma elipsóide, pois há um que multiplica . Então agora é só desenhar, parça!
