Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.3 - Ex. 2 c
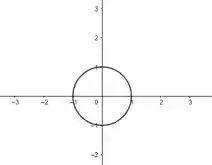
Desenhe a superfície de nível correspondente a
c)
Passo 1
Perceba que nossa função está em mas como não estamos com o nível 1 não aparece a coordenada nossa curva tá só em , e nos fornece a equação de um circulo de centro na origem e raio 1 Vamo desenhar então?
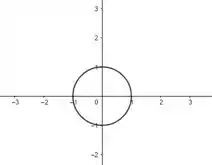
Resposta
Exercícios de Livros Relacionados
Calcule, caso exista, lim h , k → 0,0 f h , k h , k , onde f é dada por f x , y = x 3 x 2 + y 2 .
Seja f x , y =e 1 x 2 + y 2 + 1 ,s ex 2 + y 21 0 ,s e x 2 + y 2 ≥ 1 . Calcule lim x , y → 2 2 ,2 2 f x , y x 2 + y 2 - 1
Seja f x , y = 2 x y 2 x 2 + y 4 Considere a reta γ t = ( a t ,b t ) ,com a 2 + b 20 ; mostre que quaisquer que sejam a e b. lim t → 0 f (γ t ) = 0 Tente vizualizar este resultado através das curvas
Suponha que lim x , y → x 0 , y 0 f x , y =a e lim u → a g ( u ) = L , com g não definida em a em I m ⊂ D g . Prove que l i m x , y → x 0 , y 0 g f x , y = lim u → a g ( u ) Prove, ainda, que o res
Sejam γ 1 e γ 2 curvas satisfazendo as condições do exemplo 4. A afirmação : lim t → 0 f γ 1 t = l i m t → 0f γ 2 t = L ⟹lim x , y → 0,0 f x , y = L É falsa o verdadeira ? Justifuque.