Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 11
Se , determine e e interprete esses números como inclinações. Ilustre ou com um esboço à mão ou utilizando o computador.
Passo 1
Falaeee, belezinha?? Bom... o enunciado nos deu a seguinte função de duas variáveis:
Queremos determinar as derivadas parciais e , ou seja, iremos calcular as seguintes derivadas parciais, respectivamente:
E
Para isso, vamos primeiro calcular as derivadas parciais de forma geral para depois aplicarmos o ponto dado .
Mas como calculamos derivadas parciais???
Para determinar derivadas parciais, é necessário fixar as variáveis que não estão envolvidas na derivação e tratá-las como valores constantes.
Por fim, iremos esboçar um gráfico utilizando um software matemático e comentar um pouquinho ele, belezinha??
Agora bora lá!! 😉
Passo 2
Seja .
Para determinar fixamos o valor de e derivamos em relação a . Portanto, obtemos:
Assim, aplicando a derivada da soma, obtemos:
Sabendo que a derivada de uma constante é zero (lembre-se que o aqui também é uma constante) e aplicando a regra da potência, temos:
Passo 3
Agora vamos determinar a derivada em .
Para determinar fixamos o valor de e derivamos em relação a . Portanto, obtemos:
Assim, aplicando a derivada da soma, obtemos:
Sabendo que a derivada de uma constante é zero (lembre-se que o aqui também é uma constante) e aplicando a regra da potência, temos:
Passo 4
Agora basta substituir os valores de e , respectivamente, nas derivadas parciais encontradas.
Para a derivada em , temos:
E, para a derivada em , temos:
Agora vamos interpretar o que fizemos!!
Passo 5
Bom... em determinado ponto, ela representa a inclinação da reta tangente ao ponto da curva obtida quando “cortamos” a função com um plano de um valor ou constantes.
Veja as imagens a seguir, as quais irão auxiliar no seu entendimento.
Quando a derivada parcial é em relação a :
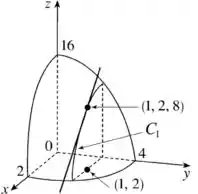
Perceba que na direção do eixo , a inclinação da superfície é de . Se nos movermos uma unidade positiva na direção a partir do ponto , a função diminuirá em unidades.
Agora, quando a derivada parcial é em relação a :
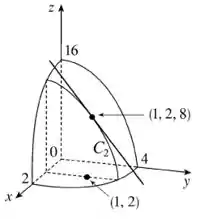
Perceba que na direção do eixo , a inclinação da superfície é de . Se nos movermos uma unidade positiva na direção a partir do ponto , a função diminuirá em unidades.