- Determine o conjunto dos pontos de acumulação do conjunto dado.
d)
Passo 1
Graficamente, essa função ficaria,
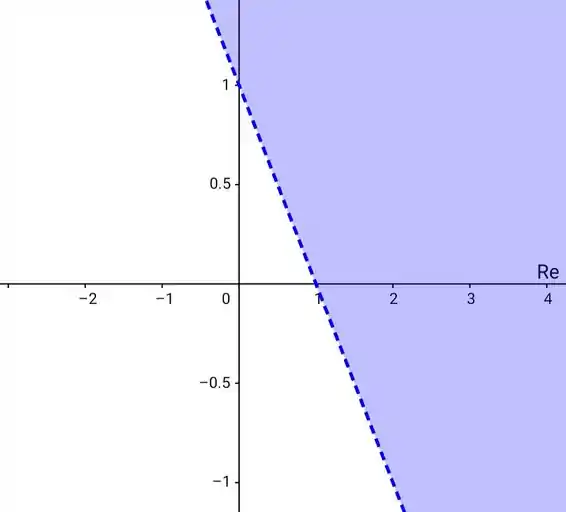
Os pontos de acumulação seriam os pontos para 'preencher' esse pontilhado.
Graficamente,
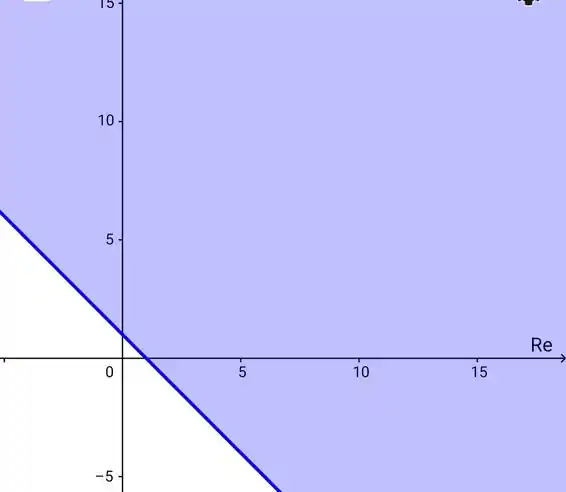
d)
Graficamente, essa função ficaria,

Os pontos de acumulação seriam os pontos para 'preencher' esse pontilhado.
Graficamente,
