Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 35
Determine o volume do sólido por subtração de dois volumes.
O sólido delimitado pelos cilindros parabólicos e e pelos planos , .
Passo 1
E aii, galera?
Nessa questão a gente precisa determinar o volume de um sólido, usando subtração de dois volumes!
Ou seja, o sólido que a gente quer calcular é um sólido que foi retirada uma parte dele .
O que a gente vai fazer é: descobrir quem são esses sólidos e , a partir das superfícies que o problema nos deu, e calcular o volume:
Lembrando que um sólido limitado pelo gráfico de uma função e o plano , em um domínio tem o volume dado pela integral:
Passo 2
Para calcular o volume, a gente vai usar os planos
Como gráficos das funções que vamos integrar.
As curvas no plano
Vão delimitar a região de integração .
Então primeiro vamos reescrever as equações dos planos como funções de e , isolando o :
Agora vamos definir a região de integração . Esboçando as curvas e no plano :
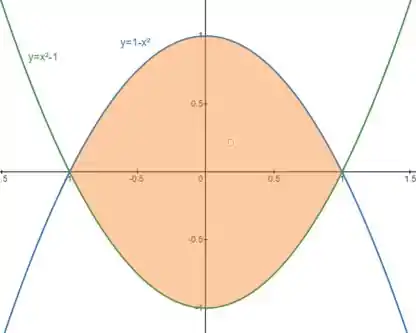
Essa região entre as curvas é definida por:
Passo 3
A gente precisa saber agora qual função ( ou ) está acima de qual dentro dessa região de integração. Porque isso vai definir qual dessas funções gera o sólido e qual gera o .
Primeiro, achamos aonde esses planos se interceptam:
Isso é a reta:
Essa reta não passa pelo domínio :
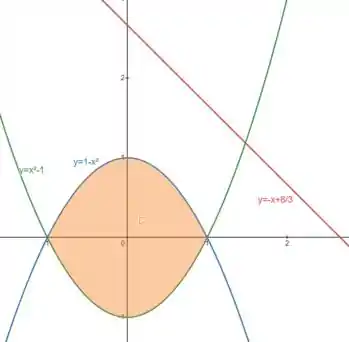
O que indica que nesse domínio se em um ponto, isso será verdade para todo (ou vice versa).
Então vamos testar no ponto :
Portanto, em todo domínio , .
Voltando pra expressão que representa o volume dos sólidos:
Então vai ser o sólido abaixo de , pois é o sólido maior, e o sólido abaixo de :
O volume de então vai ser:
Como as duas integrais estão sobre o mesmo domínio, a gente pode juntar em uma só:
Então:
Agora nosso problema vai ser só calcular essa integral!
Passo 4
Como nosso domínio é
A gente pode reescrever a integral como uma integral iterada:
Calculando primeiro em função de , mantendo constante:
Como e são constantes (em função de ), vamos juntas os dois para a integração:
Substituindo nos limites de integração:
Como , a diferença desses dois termos vai dar , e:
Resolvendo a integral:
Então: