Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 55
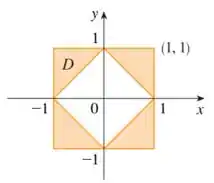
Expresse como uma união de regiões de tipo I ou do tipo II e calcule a integral.
Passo 1
Fala, galera! Como cês tão?
A questão quer que a gente descreva a região dada na imagem como regiões do tipo I ou II e que a gente calcule:
Nada melhor do que começarmos recapitulando o que são essas regiões e seus respectivos tipos:
- Regiões do Tipo I: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
- Regiões do Tipo II: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
- A reta superior, podemos ver que é constante e seu valor nunca sai de . Então ela é:
- A reta inferior passa pelos pontos e , então vamos descobrir sua equação:
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar abaixo da outra no eixo , assim a região fica confinada entre e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar antes da outra no eixo , assim a região fica confinada entre e .
A questão pede para escrevermos a integral sobre a região dada e em seguida calculá-la. Neste caso, vamos quebrar a integral em quatro partes, uma em a cada quadrante.
Além disso, note que o integrando é uma função par, e a região de integração é simétrica. Desta forma, podemos calcular a integral apenas sobre a região (primeiro e quarto quadrantes, mas não podemos esquecer de multiplicar o resultado por .
Caso não se lembre uma função é par se para todos os no seu domínio. Resumindo: uma função é par se, quando você substitui por , o resultado não muda.
Vamos ver como fica isso!
Passo 2
Vamos escrever nossa região como Tipo . Ou seja, entre duas constantes e entre duas funções.
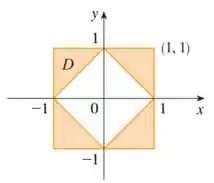
No primeiro quadrante, temos que varia de a , enquanto varia entre duas retas:
A equação da reta é:
Encontrando :
Substituindo as coordenadas dos pontos:
Para achar é só substituirmos um dos pontos na equação. Aqui usaremos :
Então:
Nossa reta será:
Aplicando nossos limites de integração:
Passo 2
Já no quarto quadrante, varia de até . Assim,
Como comentamos, temos uma figura simétrica de uma integral de uma função par, então se calcularmos somente a metade da figura e multiplicarmos por chegamos no mesmo resultado.
Desta forma,
Passo 3
Agora vamos resolver a integral. Fazendo a primeira integral em , que é a integral de dentro. Aqui mantemos como constante:
Aplicando os intervalos de integração:
Portanto, simplificamos, temos as integrais de fora em :
Desta forma, temos que: