Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 40

Use um sistema de computação algébrico para determinar o volume exato do sólido.

Entre os paraboloides z = 2 x 2 + y 2 e z = 8 - x 2 - 2 y 2 e dentro do cilindro x 2 + y 2 = 1 .

Passo 1

E aiii turma, tudo bem?

Bom, precisamos determinar o volume exato de um sólido usando um sistema de computação algébrico.

Esse sólido está entre os dois paraboloides:

z = 2 x 2 + y 2

z = 8 - x 2 - 2 y 2

E dentro do cilindro:

x 2 + y 2 = 1

E agora, como resolvo essa?

Vamos lembrar como é a expressão do volume:

V = ∬ D z ( x , y ) d A

Onde, z ( x , y ) é a função que delimita a região, d A = d x d y e D é nossa região de integração.

Precisamos montar nossa integral de volume, porém antes vamos fazer um esboço gráfico para sabermos qual função de z ( x , y ) está acima e abaixo da região. Então, podemos fazer:

z x , y = z a c i m a - z a b a i x o

Precisamos encontrar nossa região D , que compreende os intervalos de integração.

Como temos um cilindro:

x 2 + y 2 = 1

x 2 + y 2 = r 2

É mais interessante escrevermos em coordenadas polares. Nesses casos vamos ter:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Como é um cilindro inteiro de r = 1 , sabemos que os intervalos serão:

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Para resolver a integral, você pode usar a calculadora online WolframAlpha.

Bora lá!!!

Passo 2

Vamos começar plotando os gráficos dos paraboloides e do cilindro, para compreender nossa região.

Utilizando o Geogebra, obtemos:

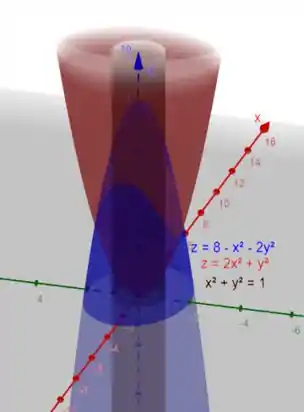
Observe que o paraboloide em azul está acima e o paraboloide em vermelho abaixo, logo:

z a c i m a = 8 - x 2 - 2 y 2

z a b a i x o = 2 x 2 + y 2

Para transformar em coordenadas polares, vamos substituir por:

x = r cos ⁡ θ

y = r   s e n   θ

Sabemos que s e n 2 θ + cos 2 ⁡ θ = 1 . Logo temos:

z a c i m a = 8 - r 2

z a b a i x o = 2 r 2 cos 2 ⁡ θ + r 2 s e n 2 θ

Lembrando que o domínio de integração D é:

D = r , θ ∈ R 2   0 ≤ r ≤ 1 ,     0 ≤ θ ≤ 2 π }

Assim a integral que dá o volume será:

V = ∫ 0 2 π ∫ 0 1 8 - r 2 - 2 r 2 cos 2 ⁡ θ + r 2 s e n 2 θ     r d r d θ

Passo 3

Agora precisamos determinar o volume através de um sistema de computação algébrico.

V = ∫ 0 2 π ∫ 0 1 8 r - r 3 - 2 r 3 cos 2 ⁡ θ + r 3 s e n 2 θ     d r d θ

Vamos utilizar a calculadora online Wolfram Alpha.

Atraves do input: Integrate[Integrate[(8r-r^3- 2r^3cos θ ^2-r^3 sen θ^2 ),{r,0,1}],{θ,0,2π}].

Vamos obter:

V = 27 π 4

Resposta

V = 27 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ 0 y f ( x , y ) d x d y
Use um sistema de computação algébrica para determinar o volume exato do sólido.Limitado por z = 1 - x 2 - y 2 e z = 0 .
Use um sistema de computação algébrica para determinar o volume exato do sólido.Abaixo da superfície z = x 3 y 4 + x y 2 e acima da região limitada pelas curvas y = x 3 - x e y = x 2 + x para x ≥ 0 .
Determine o volume do sólido por subtração de dois volumes.O sólido limitado pelo paraboloide cilíndrico y = x 2 e pelos planos z = 3 y , z = 2 + y .
Determine o volume do sólido por subtração de dois volumes.O sólido sob o plano z = 3 , acima do plano z = y e entre os cilindros carabólicos y = x 2 e y = 1 - x 2 .