Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 18

Esboce o sólido cujo volume é dado pela integral e calcule-a.

∫ 0 2 π ∫ π / 2 π ∫ 1 2 ρ 2 sen ⁡ ϕ d ρ   d ϕ   d θ

Passo 1

Show de bola, galera! Nosso primeiro passo será identificar a região cujo volume vamos calcular em função dos limites de integração, beleza?

Vamos lá...Olhando para os nossos limites de integração, vemos que a região sólida na qual estamos interessados é dada por:

R = ρ , θ , ϕ | 1 ≤ ρ ≤ 2 ,   0 ≤ θ ≤ 2 π , π 2 ≤ ϕ ≤ π

Esboçando essa região, temos:

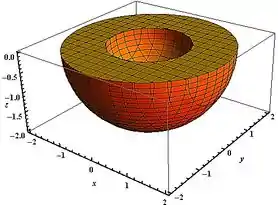
Show....Agora partiu calcular a integral?

Passo 2

Como o nosso integrando ρ 2 sen ⁡ ϕ é um produto de funções de uma única coordenada podemos dizer uma  g ρ = ρ 2  e uma  h ϕ = sen ⁡ ϕ , podemos calcular a integral da seguinte forma:

∫ 0 2 π ∫ π 2 π ∫ 1 2 ρ 2 sen ⁡ ϕ d ρ d ϕ d θ = ∫ 0 2 π d θ ⏟ θ 0 2 π ∫ π 2 π sen ⁡ ϕ d ϕ ⏟ - cos ⁡ ϕ π 2 π ∫ 1 2 ρ 2 d ρ ⏟ ρ 3 3 1 2 = 2 π - - 1 7 3 = 14 π 3

Resposta

∫ 0 2 π ∫ π 2 π ∫ 1 2 ρ 2 sen ⁡ ϕ d ρ d ϕ d θ = 14 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use coordenadas esféricas.Encontre o volume da parte da esfera ρ≤a que fica entre os cones ϕ = π 6 e ϕ = π 3 .
Use coordenadas esféricas.
Calcule o valor de: ∭ E x 2 + y 2 + z 2 d V Onde E fica acima do cone z = x 2 + y 2 e entre as esferas x 2 + y 2 + z 2 = 1 e x 2 + y 2 + z 2 = 4 .
Use coordenadas esféricas.
Encontre a massa e centro de massa de um hemisfério sólido com raio a e densidade proporcional a distância de sua base.