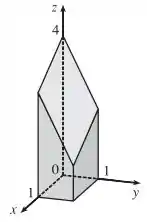
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Beleza, galera? O comando aqui até que é simples.
Temos uma integral dupla que nos da o volume de um sólido. O que a gente quer é o esboço dessse sólido.
E como fazemos isso?
Vamos começar relembrando como usamos uma integral dupla que calcular o volume de um sólido e o que cada termo representa.
Lembra que quando integramos uma função , só de uma variável mesmo, a gente encontra a área sobre a curva?
No caso de uma função de duas variáveis , se a gente integrar, a gente encontra o volume sobre a superfície. E no caso, aí vai ser uma integral dupla e não simples. Então vamos a teoriazinha que você deve levar pra sua prova.
O volume abaixo da superfície e acima do plano , dentro do retângulo , é dado por:
Sendo esse retângulo aí dado pelos intervalos de integação das variáveis e .
Agora vamos pro passo 2, enter isso aí melhorzinho na prática, olhando pra nossa integral.
Passo 2
Então vamos encarar o nosso volume:
Nosso integrando, moleza:
Ele vai nos dar a superfícia e limita o nosso sólido superiormente (por cima). No caso, essa é a equação de um plano. Então isso quer dizer, que o nosso sólido vai estar abaixo desse plano.

Agora a região , que, como já vimos no passo 1, é dada pelos limites de integração. Ambas as integrais vão de até . Mas lembra que tem uma ordem aí, que depende de quem vem antes no final da integral. No caso temos , então a integral de dentro é em e a de fora em .
Sendo assim a região é:
E a parte de baixo? Bem, já por definição, nessa fórmula, que nos dá o volume abaixo da superfície, temos que o sólido é delimitado pelo plano ou .
Passo 3
Agora juntando as informações que encontramos, esse sólido é delimitado:
- Por cima pelo plano:
- Por baixo pelo plano:
- Lateralmente pelo retângulo: e
E assim chegamos que nosso sólido é esse bonitão aqui!
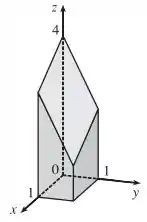
É como se a gente pegasse o retângulo na base e esticasse ele pra cima, como que pra formar um prisma retangular. Mas em vez de chegar numa base paralela, a gente corta ele no nosso plano inclinado ;D
Entendeu tudo? Bora pra próxima.
Resposta