Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.2 - Ex. 24
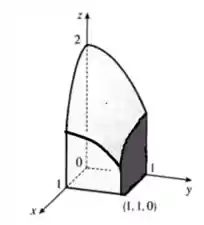
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Beleza, galera? Vamos começar mais uma!!
Nosso objetivo, é esboçar um solido. Cujo seu volume é dado pela seguinte integral iterada:
Vamos pensar juntos um pouco, beleza?
Olhe para os limites de integração. Observe que temos um retângulo, onde , . Com isso podemos concluir que o sólido está na região do retângulo.
A fórmula geral de volume é a seguinte:
Onde, é a função que delimita a região, e é nossa região de integração.
Agora observe, que o sólido vai ser delimitado pelo paraboloide circular .
Com essas informações, podemos colocar mão na massa. Pois já temos as duas regiões que delimitam o volume do sólido: o retângulo e o paraboloide.
Passo 2
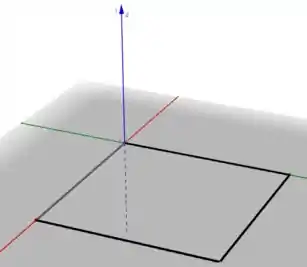
Vamos começar analisando a região do retângulo.
Temos que: , . Isso nos dá o seguinte gráfico:
Para o paraboloide, temos a seguinte equação:
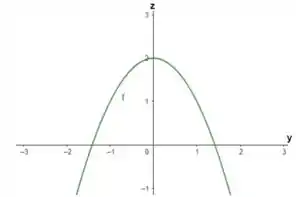
Vamos analisar no plano , fazendo .
Nossa equação fica:
Isso é uma parábola com cavidade para baixo. Fazendo o gráfico temos:
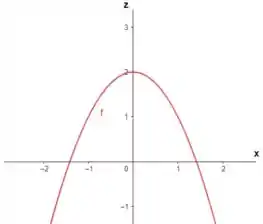
Agora vamos analisar no plano , fazendo .
Nossa equação fica:
Também é uma parábola com cavidade para baixo. Fazendo o gráfico temos:
Passo 3
Agora já podemos pensar em como vai ficar isso no tridimensional.
Nossa região vai ficar com essa cara:
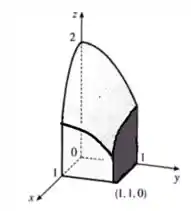
E observe que temos exatamente as curvas que mencionamos antes, o retângulo no plano e as parábolas nos planos e .
Resposta
