Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 10
Um mapa de contorno de uma função é apresentado. Utilize-o para estimar e .
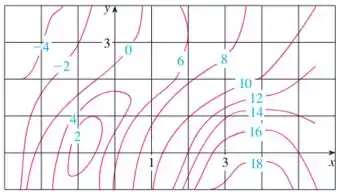
Passo 1
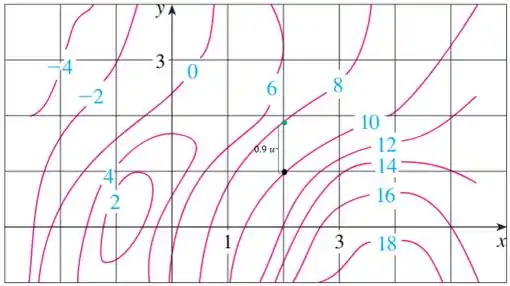
Eaee, belezinha?? Bom... o enunciado nos deu o seguinte mapa de contorno de uma função :
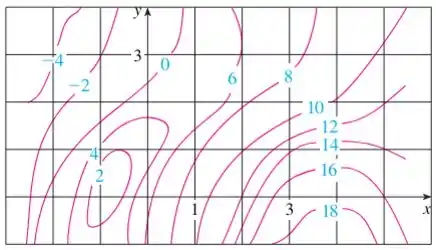
Queremos estimar as derivadas parciais e no ponto .
Em outras palavras, queremos determinar essas derivadas nesse ponto:
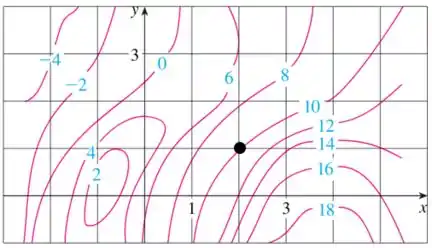
Obs: note que o valor da função no ponto dado é .
Para isso, temos que lembrar que para resolver derivadas parciais, a gente fixa uma variável (fazendo ela como constante) e deriva em relação a outra. E depois faz o mesmo com as variáveis trocadas.
Aqui é basicamente isso!! A gente primeiramente vai fixar a variável e verificar a variação em . Em seguida a gente vai fazer o contrário!!
Aaah.. lembre-se que estamos trabalhando com estimativas, viu?? Então vamos utilizar nosso olhômetro para estimar haha!!
Agora bora lá!! 😉
Passo 2
Primeiramente vamos fixar e vamos fazer uma média dos valores da função no sentido positivo de .
Perceba que inicialmente o valor de é e o seguinte é após aproximadamente unidades de :
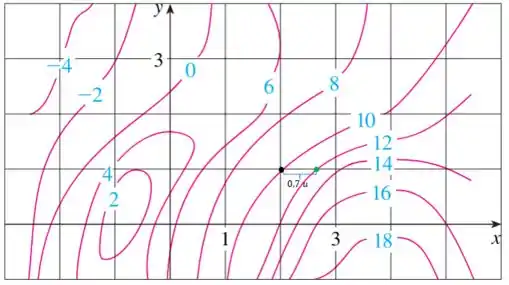
Assim, a nossa derivada é dada por:
Agora vamos fazer o mesmo para !! 😉
Passo 3
Agora vamos vamos fixar e vamos fazer uma média dos valores da função no sentido positivo de .
Perceba que inicialmente o valor de é e o seguinte é após aproximadamente unidades de :
Assim, a nossa derivada é dada por: