Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 94
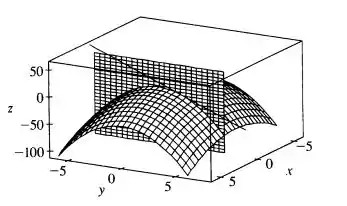
O paraboloide intercepta o plano em uma parábola. Determine as equações paramétricas para a reta tangente a essa parábola no ponto . Use um computador para fazer o gráfico do paraboloide, da parábola e da reta tangente em uma mesma tela.
Passo 1
Olá, como vai? Espero que esteja bem, vou te ajudar a resolver essa atividade hoje.
Temos a paraboloide:
Que intercepta o plano:
E nos gera uma parábola.
Queremos encontrar as equações paramétricas tangentes a essa parábola no ponto:
Para isso primeiro devemos encontrar a equação da parábola, para isso devemos subsituiro do na equação da paraboloide.
Depois disso deveremos lembrar que a equação da reta é dada por:
Onde é o coeficiente angular no ponto:
Parai isso deveremos calcular:
Para a equação da parábola. O ponto iremos descobrir considerando que:
Pertence a essa reta, sendo assim basta substituir esse ponto nessa reta e encontramos o valor de . Se ficou confuso não se preocupe, iremos fazer tudo bem devagar e você irá entender.
Passo 2
Pessoal, se substituirmos na equação do paraboloide, encontraremos a equação da parábola de intersecção:
Para descobrirmos a inclinação da reta tangente a essa parábola, é só derivar ambos os lados da equação acima:
Como queremos descobrir as equações paramétricas da reta tangente no ponto , vamos substituir para descobrir a inclinação da reta:
Agora como o ponto pertence a reta, se substituirmos esse ponto na nossa reta, conseguiremos encontrar o valor de :
Do ponto:
Temos que nossa reta será então:
Então, as equações paramétricas serão:
Pois é o valor do nosso plano, poderemos então chamar:
Então teremos que:
Passo 3
Show! Agora vamos usar um computador para fazer o seguinte gráfico:
