Um problema de interesse na história da matemática é a de encontrar a tautócrona- a curva descrita por uma partícula deslizando livremente sob a ação apenas da gravidade, atingindo o fundo no mesmo instante independente de seu ponto de partida na curva. Esse problema apareceu na construção de um relógio com pêndulo, cujo período é independente da amplitude de seu movimento. A tautócrona foi encontrada por Christian Huygens (1629-1695), em 1673, por métodos geométricos e, mais tarde, por Leibniz e Jakob Bernoulli usando argumentos analíticos. A solução de Bernoulli (em 1690) foi uma das primeiras ocasiões em que se resolveu explicitamente uma equação diferencial. A configuração geométrica está ilustrada na figura a seguir. O ponto inicial é unido ao ponto final pelo arco . O comprimento de arco é medido a partir da origem, e denota a taxa de variação de em relação a :

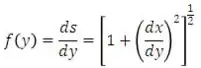(i)

Segue, então, do princípio de conservação de energia, que o tempo necessário para uma partícula deslizar de até a origem é:

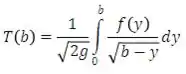(ii)

(a) Suponha que , uma constante, para cada . Calculando a transformada de Laplace da equação nesse caso e usando o teorema sobre a convolução mostre que:

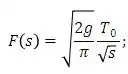(iii)

Depois mostre que:

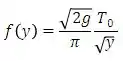(iv)

(b) Combinando as equações (i) e (iv), mostre que:

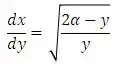(v)

Em que .

(c) Use a substituição para resolver a equação (v) e mostre que

Nosso próximo passo será utilizar a função que encontramos para chegar a uma expressão para . Vamos lá???

A equação (i) é:

Elevando os dois lados ao quadrado:

Chamando ficamos com:

E finalmente tirando a raiz dos dois lados chegamos em:

Nosso último passo devemos resolver a equação:

O exercício sugere que façamos a substituição:

A função pode ser descrita como:

Então

E chegamos à equação para a posição . Agora vamos calcular o diferencial para aplicar na equação .

Voltando à equação :

A função pode ser escrita como:

Substituindo: