Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 15.3 - Ex. 13 b
Seja a função energia potencial associada ao campo
- Uma partícula de massa 1 é abandonada na posição com velocidade . Admita que é a única força atuando sobre a partícula . Determine a posição da partícula no instante t. Desenhe a trajetória descrita pela partícula.
Passo 1
O ponto chave da questão é perceber que do campo que encontramos, temos que ele representa nossa aceleração, usando a Lei de Newton ou seja, tomando como sendo as coordenadas da função deslocamento, temos que
(*)
A questão nos dia que a partícula é abandona na posição Em outras palavras,
Além disso, tinha velocidade nula, ou seja,
Estamos só interpretando as informações do problema, ok?
Passo 2
De (*), temos que
Pela lei de Newton, Daí,
O que significa que nossa parametrização é da forma
Usando a identidade
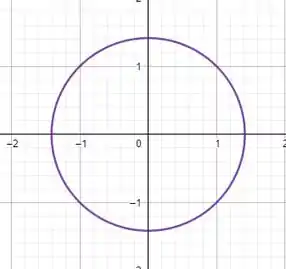
A imagem de é um circunferência de centro na origem em raio
Resposta
Uma circunferência de centro na origem em raio
Exercícios de Livros Relacionados
Considere a curva C de intersseção das superfícies definidas de equações x 2 - 2 x z + y 2 z = 3 e 3 x y - 2 y z = - 2 . Determine:Um vetor tangente a C em ( 1 , - 2,1 ) .
12-Mostre que em todos os pontos da interseção da semiesfera de equação x 2 + y 2 + z 2 = 16 ,z ≥ 0 , com o cone de equação z = x 2 + y 2 , os vetores normais a estas superfícies são ortogonais.
14. Seja z = f ( x , y ) uma função de classe C 1 . O gráfico de f ( x , y ) pode ser considerado como a superfície de nível de nível F x , y , z = f x , y - z = 0 . Mostre que as equações do plano ta
Existe uma direção u na qual a taxa de variação de ƒ(x, y) = x2 – 3xy + 4y2 em P(1, 2) é igual a 14? Justifique sua resposta.
Derivadas direcionais e componentes escalares Como é a derivada de uma função diferenciável ƒ(x, y, z) em um ponto P0 na direção de um vetor unitário u relacionado ao componente escalar de (¥ƒ)P0 na d