Utilize coordenadas polares para determinar o volume do sólido dado.
Acima do cone e abaixo da esfera
Passo 1
Beleza, galera?
O comando aqui é simples: calcular o volume de um sólido.
E o enunciado nos diz explicitamente que é o sólido que fica acima do cone:
E abaixo da esfera:
Vamos começar olhando pra cara disso, pra gente já sair do matematiquês e conseguir ver algo acontecendo:
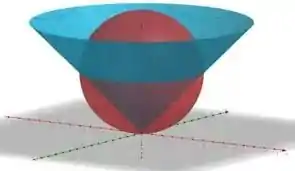
Agora vamos relembrar da nossa teoria... você se lembra que lá em cálculo 1, a gente viu que a área entre duas curvas é a integral da curva de cima menos a curva de baixo?
Pois a gente consegue extrapolar isso aqui pra volumes e integrais duplas. No caso, o volume entre duas superfícieis vai ser a integral dupla da superfície de cima menos a superfície de baixo... Mas se ficou confuso, agora vou ser mais específica.
Seja um sólido abaixo da superfícia e acima de outra superfície , então o seu volume será:
Então o intervalo de baixo pra cima, ou em , ta representado aqui no nosso integrando . E lateralmente, os intervalos pra e formam a região e vão aparecer nos nossos limites de integração.
Mas o enunciado não fala nada sobre isso, e agora?
Bem, se ele não fala nada, então os limites vão ser dados pela interseção das superfícies (o cone e a esfera). Então é só fazer:
Então precisamos:
- Definir os limites de integração, fazendo ;
- Definir o integrando ;
- Converter pra coordenads polares;
- Calcular a integral.
Aaaah já tava esquecendo da mudança de coordenadas neeeee... Pois pra você respirar, vou falar disso no passo 2.
Passo 2
O enunciado nos dá uma orientação específica: usar coordenadas polares. Então antes de qualquer coisas, vamos relembrar as relações entre as coordenadas cartesianas e polares:
Mas não é só isso e aqui que mora o erro!!! O diferencial da área também vai ter um fatorzinho de conversão, que você não pode esquecer.
Em coorenadas cartesianas, como já vimos no passo 1, a integral vai ficar assim:
Quando convertemos pra coordenadas polares, vai aparecer um termo extra ali dentro do integrando e fica desse jeito aqui:
A regiaõ é a mesma, assim como as superfícies e . Mas tudo aqui estará descrito em função de e , nossas coordenadas polares.
Passo 3
Agora vamos definir quais vão ser os limites de integração e, pra isso, vamos igualar os valores de das duas superfícies dadas pelo enunciado:
Reescrevendo a equação da esfera:
Igualando:
E essa é a equação de uma circunferência de raio .
Agora a gente pode prosseguir com a análise em coordenadas cartesianas pra fazer a conversão pra coordenadas polares. Mas vamos ser mais espertos do que isso, porque a gente já tem o termo perfetinho pra converter.
Da coordenadas cartesianas pra polares, temos , então nossa relação fica:
E como a coordenada nunca é negativa, porque ela representa o raio, já temos seu intervalo:
E o intervalo em ? Qual vai ser?
Nenhuma restrição foi mencionada. Tanto o cone quanto a esfera fazem a volta completa, então:
Pronto, temos nossos limites de integração. E só pra você sacar bem das nomenclaturas, a região de integração é o círculo de raio .
PS. Se você tiver pensando “nossa, muito mais fácil que usar as coordenadas cartesianas”. Sim, mas não é a toa que o enunciado nos pediu pra converter. A gente precisa, pelo menos tentar, usar o sistema de coordenads mais conveniente, que torna o nosso cálculo mais simples.
Passo 4
Agora vamos determinar a função a ser integrada:
Sempre vai ser a curva “de cima” menos a curva “de baixo”, então é a esfera menos o cone:
Convertendo pra coordenadas polares:
Novamente, ficou bem mais simples... nenhuma surpresa! É pra isso mesmo que estamos convertendo.
Logo, nossa integral vai ficar assim:
FINALMENTEEEEEEEE!
Conseguimos representar nosso volume como uma integral. Agora vamos integrar. Juro pra você que falta pouco! (mas só falta pouco porque convertemos pra polares, aí o cálculo é fácil)
Passo 5
Vamos lá:
Como as nossas variáveis aqui são bem independentes (os limites de integração são constantes e não funções), então nós podemos separar a integral dupla no produto de duas integrais simples, calculando cada termo com seu integrando, respectivamente:
Resolvendo em :
Pra resolver em , vamos primeiro separar essa subtração:
O segundo termo é moleza:
E no primeiro termo vai ter que rolar uma substituiçãozinha. Vamos fazer e, logo, :
Somando os dois resultados, vamos ter a integral em :
Agora lembra que a gente tinha separado o volume no produto da integral de e ? Pois então vamos multiplicar os resultados:
E finalmente temos nossa resposta!!! Ufa! Agora vai beber uma água antes de partir pro próximo exercício.