Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 51

Utilize a fórmula de mudança de variáveis e uma transformação adequada para calcular ∫ ∫ R x y   d A , onde R é o quadrado com vértices ( 0 ,   0 ) ,   ( 1 ,   1 ) ,   ( 2 ,   0 )   e   ( 1 ,   - 1 ) .

Passo 1

E aí meus queridos, tudo bom com vocês?

Queremos calcular a integral ∬ R x y   d A , onde R é um quadrado rotacionado no plano x y , conforme mostra a figura abaixo:

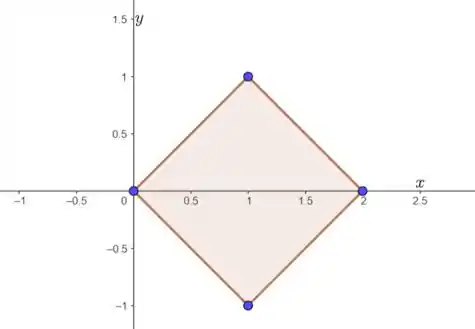
Quadrado rotacionado

A questão seria bastante fácil se esse quadrado não estivesse rotacionado, concorda? Então, nossa substituição será justamente nesse sentido. Repare nas equações das retas (ver figura abaixo):

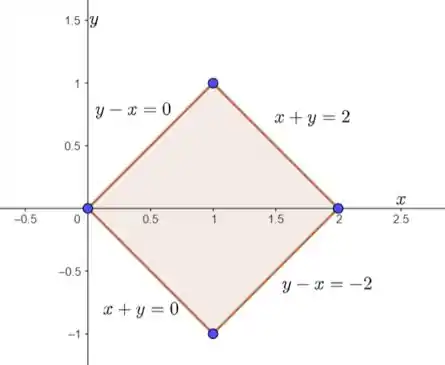
Equações das retas

Assim, será bastante natural tomarmos as seguintes substituições

u = y - x v = x + y

Pois, nesse caso u ficará limitado entre - 2 ≤ u ≤ 0 e v entre 0 ≤ v ≤ 2 !

Passo 2

Vamos aplicar as ideias explicadas anteriormente. De início, precisamos encontrar x e y em função de u e v , e não u e v em função de x e y . Para isso, vamos somar as duas equações.

u + v = 2 y ⟹ y = 1 2 u + v

Dessa forma,

x = v - y = v - 1 2 u + v

x = 1 2 v - u

Segue então:

x = 1 2 - u + v y = 1 2 u + v

Agora, vamos calcular o jacobiano dessa transformação:

∂ x , y ∂ u , v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Substituindo as derivadas parciais:

∂ x , y ∂ u , v = - 1 2 1 2 1 2 1 2

Calculando o determinante da matriz:

= - 1 2 ⋅ 1 2 - 1 2 ⋅ 1 2 = - 1 2

Assim, temos que:

∬ R x y   d x   d y = ∬ R * 1 2 u + v ⋅ 1 2 - u + v ⋅ ∂ x , y ∂ u , v   d u   d v

Substituindo o determinante e simplificando:

∬ R x y   d x   d y = 1 8 ∬ R * v 2 - u 2   d u   d v

Agora, precisamos encontrar a nova região de integração R * .

Passo 3

A nova região será:

R * = u , v :   - 2 ≤ u ≤ 0   e   0 ≤ v ≤ 2

Então nossos limites de integração, serão:

∬ R x y   d A = 1 8 ∫ 0 2 ∫ - 2 0 v 2 - u 2 d u   d v

Resolvendo a integral de u :

= 1 8 ∫ 0 2 v 2 u - u 3 3 - 2 0 d v

Aplicando os limites de integração:

1 8 ⋅ ∫ 0 2 2 v 2 - 8 3 3 - 2 0 d v = 1 8 ⋅ 2 v 3 3 - 8 v 3 0 2

Ou seja,

∬ R x y   d A = 0

Resposta

∬ R x y   d A = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a aplicação definida por x = u v e y = v - u Calcule a a área de D .
Calcule ∫ ∫ D 2 x + 1d x d y , onde D é a região no primeiro quadrante do plano x y limitada por y = x 2 , y = x 2 + 1 , x + y = 1 e x + y = 2 .
Considere a aplicação definida por x = u v e y = v - u Determine a imagem D no plano x y do retângulo R no plano u v de vértices 0,1 , 1,1 , 1,2 e 0,2 .
Calcue ∫ ∫ D cos ⁡ x - y x + y d x d y , onde D é a região do plano x y limitada por x + y = 1 , x = 0 e y = 0 .
Considere a aplicação g definida pelas equações x = u + v e y = v - u 2 Utilizando g , calcule ∫ ∫ D x - y + 1 4 - 1 2 d x d y , onde D é a imagem no plano x y da região Q no plano u v limitada pelas