Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 1g
- Verifique quais dos conjuntos a seguir são abertos em
g)
Passo 1
Graficamente, essa função ficaria,
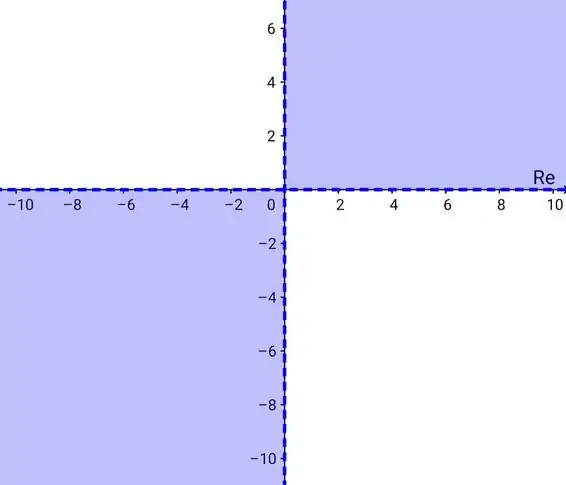
Como tem pontilhado, o conjunto é aberto.
Resposta
É aberto.
Exercícios de Livros Relacionados
Verifique se a função é homogênea. Em caso afirmativo, determine o grau de homogeneidade. f x , y = x 4 + y 4
5. Verifique se a função é homogênea. Em caso afirmativo, determine o grau de homogeneidade.a) f x , y = x 3 + 2 x y ² x 3 - y ³ ² ³
Suponha que f: IR² → IR seja homogênea do grau 2 ef a , b = a para todo ( a , b ) , com a 2 + b 2 = 1 . Calcule: f 0 , 3
Seja f: IR² → IR uma função linear. Sabendo que f 1,0 = 2ef 0,1 = 3 , calcule f x , y .
Suponha que f: IR² → IR seja homogênea do grau 2 ef a , b = a para todo ( a , b ) , com a 2 + b 2 = 1 . Calcule: f x , y ,( x , y ) ≠ ( 0,0 )