Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 1d
- Verifique quais dos conjuntos a seguir são abertos em
d)
Passo 1
Graficamente, essa função ficaria,
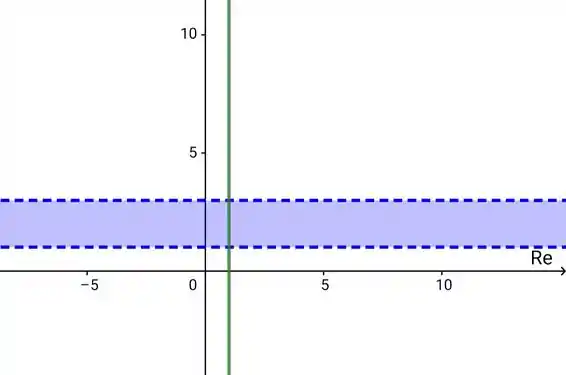
Como tem o pontilhado, significaria que o conjunto é aberto. Mas quando olhamos para a interseção, vemos que isso não é possível. Isso porque a interseção são os pontos sobre a reta x=1 que estão entre os valores de y dentro do intervalo de 1 a 3. É como se estivéssemos cortando a reta em verde e pegando apenas o que está dentro do pontilhado, ok?
Mas aí que vem o problema: qualquer ponto sobre a reta que você pegue terá uma “bola aberta” (como o livro diz) pegando valores de fora da reta, ou seja, fora da nossa região de interseção, pois aí não seriam ponto em que x=1.
Logo, temos um conjunto não aberto.
Resposta
Não é aberto.
Exercícios de Livros Relacionados
Verifique que, para a função de produção de Cobb-Douglas P L , K = 1,01L 0,75K 0,25 discutida no Exemplo 3, a produção dobrará se as quantidades de trabalho e a de capital investido forem dobradas. De
O índice I de temperatura-umidade (ou simplesmente humidex) é a temperatura aparente do ar quando a temperatura real é T e a umidade relativa é h , de modo que podemos escrever I = f ( T , h ) . A tab
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -
O que significa conjuntos no plano ou no espaço serem abertos? E fechados? Dê exemplos. Dê exemplos de conjuntos que não são nem abertos nem fechados.