Deduza a fórmula de tensão normal total para o ponto B levando em consideração a figura dada abaixo. Leve em consideração os sinais e orientações dos vetores.
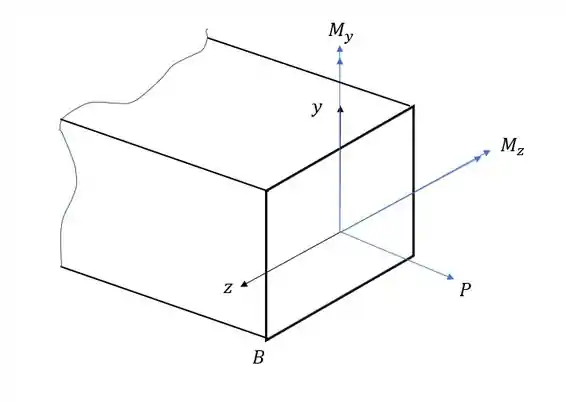
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 3 esforços nessa seção, dois esforços de flexão e um esforço normal, logo essa é a dica de que a nossa fórmula final deverá apresentar 3 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Por fim a última analise é um macete para verificarmos se acertamos ou não os sinais da fórmula.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
E por fim quando temos a ação de um esforço normal usamos a fórmula
Agora vamos entender a nossa solução.
Passo 2
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
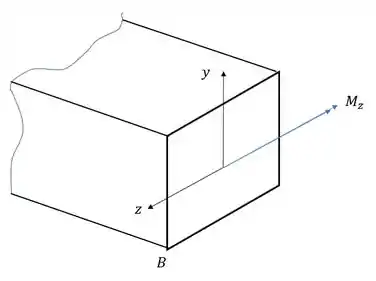
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 3
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
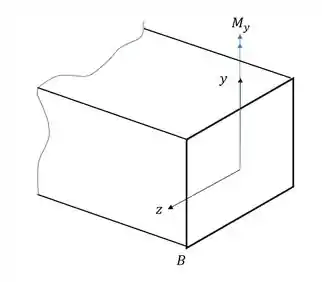
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do momento fletor é a mesma do eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto B está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 4
Passo 5
Passo 6
Por fim vamos analisar a parcela referente a ação do esforço normal
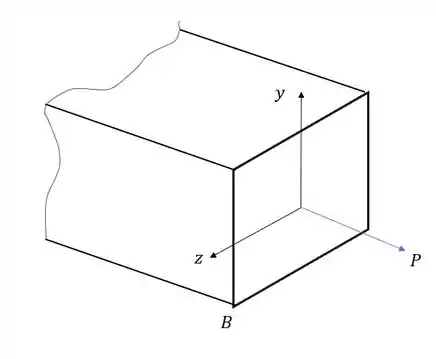
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do normal é a mesma do sentido de tração, logo,
Como a área não tem sinal, a parcela de contribuição devido no ponto B será
Passo 7
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total normal será
Passo 8
Agora que já determinamos o valor de cada uma das contribuições de cada seção vamos usas o macete pra saber se todos os sinais que determinamos estão certinhos.
Vamos definir o seguinte, nenhuma das fórmulas possui sinal, log consideraremos tudo positivo, todos os sinais serão dados apenas pela analise de tração e compressão. Para isso vamos desenhar retângulos e os nossos momentos.
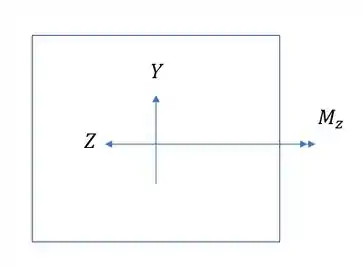
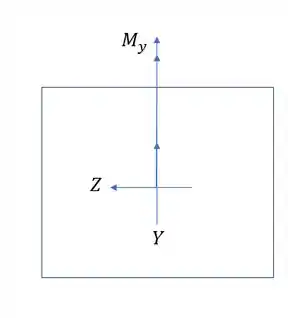
Agora só analisar quais regiões são tracionadas e quais são comprimidas
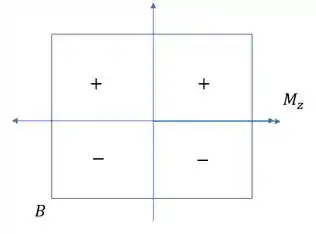
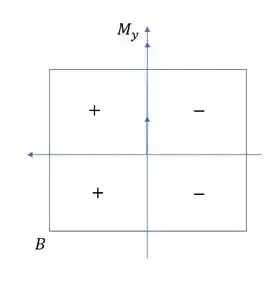
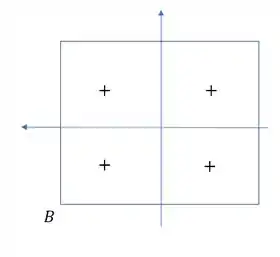
Se olharmos cada quadrante vemos que no primeiro caso B comprime, logo negativo, e nos outros dois casos traciona, ou seja, positivo.
Primeiro caso negativo
Segundo caso positivo
Terceiro caso positivo
Logo a nossa fórmula de tensões normais totais será
O que confirma que todo o cálculo que fizemos nos passos anteriores estão certinhos. Se por acaso o professor autorizar você pode usar somente o passo 6 dessa solução para resolver o problema, mas lembre-se, procure ver se o professor autoriza usar tal processo.