A seção quadrada abaixo, de lado 33cm, está sujeita a flexão assimétrica mostrada na figura. Usando seu conhecimento de decomposição vetorial, e seu conhecimento sobre tensão normal devido a flexão, determine o valor dos esforços normais no ponto A e B da peça.
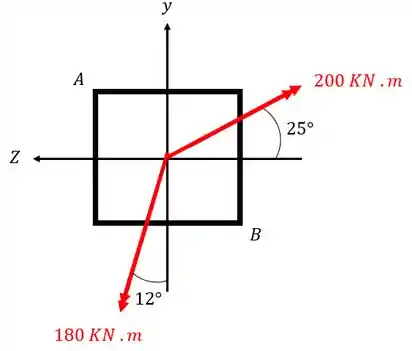
Passo 1
Para resolvermos essa questão temos que tomar cuidado com algumas coisas. A primeira é que temos 2 esforços nessa seção, os dois esforços de flexão, logo essa é a dica de que a nossa fórmula final deverá apresentar 2 parcelas, uma para cada esforço.
A segunda preocupação que devemos ter é com relação aos sinais, tanto dos eixos, quanto os dos momentos, além é claro das próprias fórmulas da flexão que apresentam os seus próprios sinais.
Dito os cuidados precisamos lembrar das fórmulas de cada direção antes de começarmos de fato a resolver o exercício.
Sabemos que quando utilizamos o momento fletor direcionado no sentido de z usamos a fórmula
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
Como a nossa seção é quadrada, já podemos determinar facilmente o valor do momento de inercia que será igual em ambas as direções, logo
Passo 2
Do jeito que os momentos fletores estão é muito complicado definir as fórmulas e os cálculos que devemos fazer, por isso, antes de qualquer coisa, vamos decompor os nossos momentos fletores, e com essa decomposição vamos poder analisar os nossos esforços.
Vamos decompor cada um dos vetores, começando pelo de
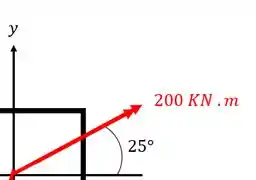
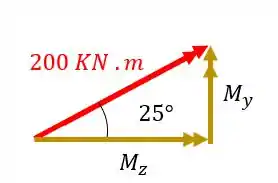
Fazendo a conta teremos que
Isolando teremos que
Decompondo agora o momento de teremos
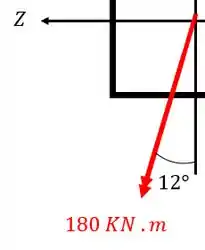
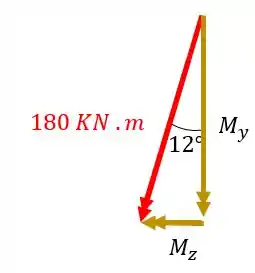
Fazendo a conta teremos que
Isolando teremos que
Olhando os vetores decompostos teremos que
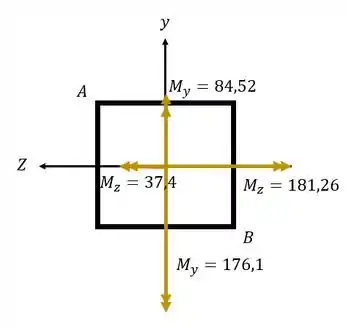
Fazendo uma soma vetorial teremos que
Então teremos
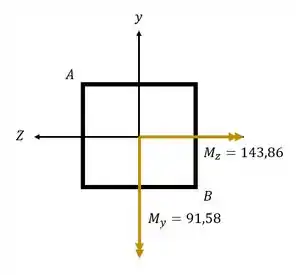
Passo 3
Vamos analisar a ação de cada esforço separadamente, primeiro vamos analisar o momento fletor na direção Z.
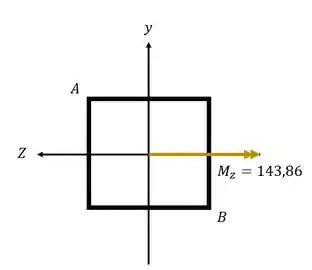
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo z, logo,
O sinal de Y é determinado pela posição do ponto que calculamos, nesse caso, em relação a Y o ponto B está em baixo e A está em cima.
Como arbitramos que Y é negativo pra baixo e positivo pra cima, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 4
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
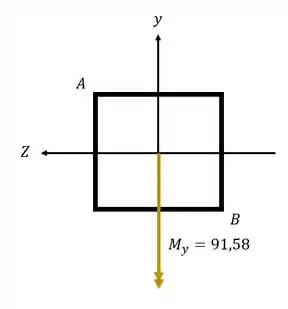
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A e B.
Primeiro vemos que a direção do momento fletor é contrário ao eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto B está na direita e A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto A e B será
Passo 5
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será