O momento é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo com a vertical. Determine a tensão no ponto , ponto e ponto .
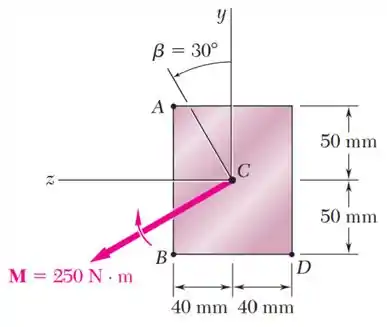
Passo 1
O que está acontecendo?
O momento pode ser decomposto em uma componente horizontal e uma componente vertical de acordo com o ângulo de indicado pelo exercício, como mostra a imagem abaixo:
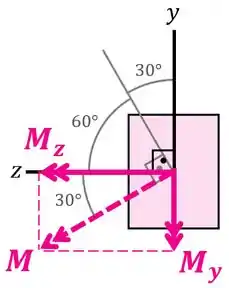
Daí que, calculando essas componentes, vamos poder descrever as tensões nessa seção transversal através da fórmula:
Sendo que nesse caso, como não temos uma força interna normal (temos só os momentos e ), essa fórmula fica assim:
E o que é que o exercício quer?
Ele quer que a gente determine as tensões :
No ponto , de posição e ;
No ponto , de posição e ;
& No ponto , de posição e .
Então, para resolver o exercício, temos que:
1. Calcular as componentes e do momento aplicado.
2. Calcular os momentos de inércia da área em relação ao eixo , , e em relação ao eixo , .
& 3. Aplicar a fórmula para os pontos , e .
Passo 2
Então primeiro, vamos calcular as componentes de .
Observando a imagem abaixo:
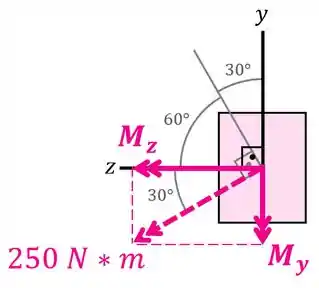
...conseguimos ver que:
E que:
Passo 3
Agora, para calcular os momentos de inércia da área e , observamos as dimensões da seção transversal:
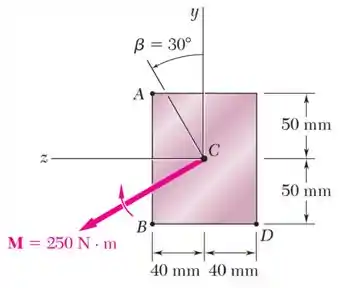
Da imagem, temos que a seção tem dimensões de .
Aqui, a fórmula do momento de inércia da área de um retângulo vale tanto para quanto para .
Além disso, nessa fórmula, a base e a altura correspondem, respectivamente, à dimensão paralela e à dimensão perpendicular ao eixo em relação ao qual se está calculando o momento de inércia da área.
Dessa forma, o momento de inércia da área em relação ao eixo vai ser:
Enquanto que o momento de inércia da área em relação ao eixo vai ser:
Passo 4
Por fim, podemos calcular a tensão em cada ponto:
Substituindo, nessas equações:
- ;
- ;
- ;
- ;
- E as posições de , e apontadas lá no passo , todas em ,
Vamos ter que:
Finalmente, calculando tudo para cada uma dessas tensões e sabendo que é o mesmo que , encontramos as nossas respostas: