Na ponta do pilar abaixo foi colocado uma carga concentrada (que representa a ação de uma viga ali apoiada). Com base em seus conhecimentos de cargas excêntricas determine a tensão normal no ponto A. O raio do pilar é de 0,80m.
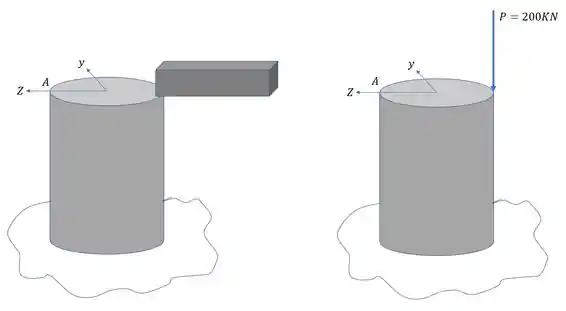
Passo 1
O primeiro passo que temos que dar é trocar as cargas mostradas por esforços e assim vermos qual fórmula usar.
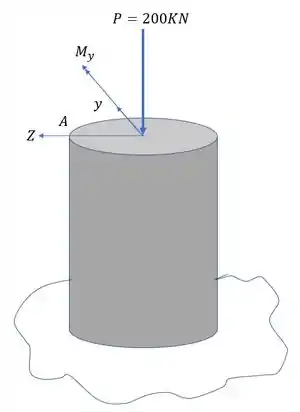
Aqui é importante ressaltar que levamos a carga P para o centro da peça e junto com ela o momento fletor causado por ela, que nesse caso é um momento fletor na direção y.
Como temos dois esforços, já sabemos que temos 2 parcelas para calcular.
Quando utilizamos o momento fletor direcionado no sentido de Y usamos a fórmula
E por fim quando temos a ação de um esforço normal usamos a fórmula
Como a nossa seção é circular, já podemos determinar facilmente o valor do momento de inercia que será igual em ambas as direções, logo
Agora vamos entender a nossa solução.
Passo 2
Agora vamos analisar a ação do esforço para o momento fletor na direção Y.
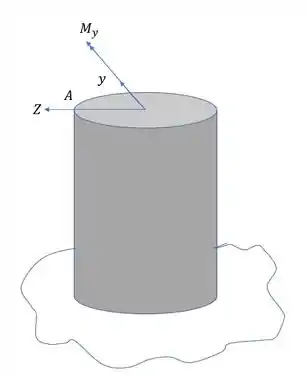
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto A.
Primeiro vemos que a direção do momento fletor é a mesma do eixo y, logo,
O sinal de Z é determinado pela posição do ponto que calculamos, nesse caso, em relação a Z o ponto A está na esquerda.
Como arbitramos que Z é negativo pra direita e positivo pra esquerda, teremos que
Como o momento de inercia não tem sinal, a parcela de contribuição devido no ponto B será
Passo 3
Por fim vamos analisar a parcela referente a ação do esforço normal
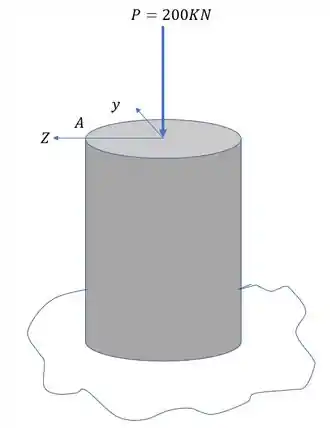
Sabemos que nesse caso a fórmula que usamos é
Precisamos agora analisar os sinais para o ponto B.
Primeiro vemos que a direção do normal é a mesma do sentido de compressão, logo,
Como a área não tem sinal, a parcela de contribuição devido no ponto B será
Passo 4
Agora que já determinamos todas as parcelas, basta somarmos todas elas na fórmula final, logo teremos que a tensão total Normal será