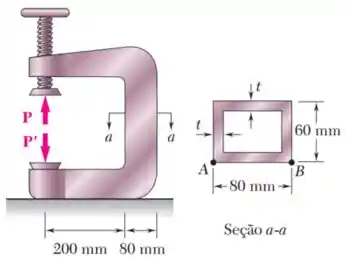
A parte vertical da prensa mostrada na figura consiste em um tubo retangular com espessura de parede . Sabendo que a prensa foi usada para prender blocos de madeira que estavam sendo colados, com uma força , determine a tensão no ponto e ponto .
Passo 1
O que está acontecendo?
As cargas , em relação ao centro da parte vertical da prensa, são excêntricas por uma distância de , como mostra a imagem abaixo:
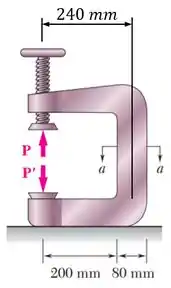
Dessa forma, definindo eixos e passando pelo centro da seção transversal dessa parte vertical:
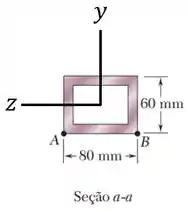
Vemos que a força excêntrica vai causar nessa seção transversal não só uma força normal como também um momento em relação ao eixo , :
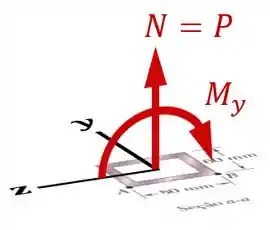
Sendo que esse momento é positivo ao longo do eixo de acordo com a regra da mão direita:

...e pode ser calculado multiplicando a força pela “excentricidade” ou pelo braço de :
E o que é que o exercício quer?
Ele quer que a gente determine a tensão nos pontos e dessa seção transversal .
Aí, pelo o que estudamos sobre cargas excêntricas, sabemos que elas geram uma tensão de acordo com a fórmula:
...dados que o eixos esteja disposto “para cima” e o eixo esteja disposto “para a esquerda” na seção transversal da peça, que foi como nós fizemos:
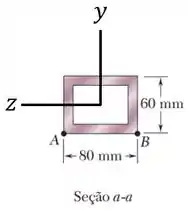
Como no nosso caso, não temos nenhum momento em relação ao eixo , a tensão nessa seção transversal vai ficar assim na realidade:
Sendo que da imagem acima, vemos que o ponto possui uma posição e que o ponto possui uma posição .
Dessa forma, para resolvermos o exercício, temos que:
1. Calcular a área e o momento de inércia da área em relação ao eixo , , dessa seção transversal, sabendo que ela possui uma espessura de parede ;
& 2. Aplicar a fórmula para os pontos e .
Passo 2
Então vamos lá!
Primeiro, observando a geometria da seção, com sua espessura :
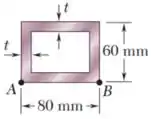
Vemos que ela é um retângulo de com um furo retangular de por .
Dessa forma, a sua área vai ser:
Passo 3
Em seguida, precisamos calcular o momento de inércia da área em relação ao eixo , , para essa seção.
Para tanto, vamos observar a sua geometria em relação ao eixo :
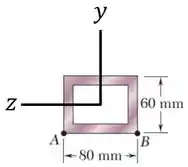
Em relação ao eixo , vemos que ela tem uma base (paralela ao eixo ) e uma altura (perpendicular ao eixo ) .
Dessa forma, o momento de inércia da área em relação ao eixo do retângulo externo dessa seção vai ser:
Mas a seção não tem só esse retângulo externo.
Ela também tem um furo, de base e altura (dimensões que vimos no passo anterior), que vai ter um momento de inércia negativo por ser um furo:
E assim, o momento de inércia da área da seção como um todo vai ser a soma dos valores de para cada elemento:
O que significa que:
Passo 4
Por fim, aplicamos a fórmula para os pontos e :
Substituindo nessas equações:
- ;
- ;
- ;
- & ;
- & ,
Vamos ter que:
Calculando tudo e sabendo que é o mesmo que , encontramos os nossos resultados finais: