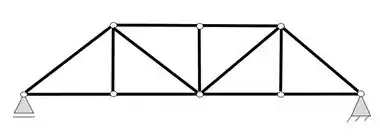
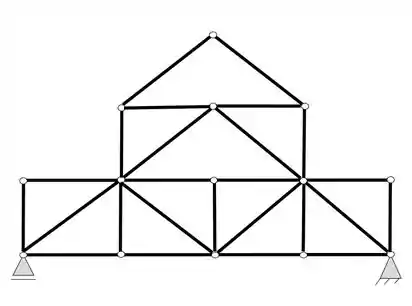
Abaixo são dadas 2 treliças, sendo a primeira uma treliça simples e a segunda uma treliça composta. Determine com base em seus conhecimentos se essas treliças são de fato treliças e também diga como elas são estruturalmente, ou seja, isostáticas, hiperestáticas ou hipostáticas.
Passo 1
Sabemos que a solução desse exercício se divide em duas analises
- Primeiro devemos analisar se os apoios da estrutura tornam ela isostática, hipostática ou hiperestática.
- Depois devemos avaliar se a nossa estrutura representa de fato uma treliça, e para representar uma treliça deve obedecer a regra dos triângulos que vimos na teoria.
Devemos tomar cuidado pois temos duas estruturas diferentes. A primeira iremos avaliar diretamente pois se trata, possivelmente de uma treliça simples, e digo possivelmente pois temos que ver se a regra irá bater. Da mesma forma faremos com a segunda, mas antes iremos dividir a estrutura e analisa cada parte dela. Se cada parte respeitar a regra, toda a estrutura irá respeitar, vamos lá então?

Passo 2
Vamos primeiro avaliar a treliça do caso a)
Vimos que a primeira coisa que devemos avaliar são seus apoios, para isso devemos nós lembrar que
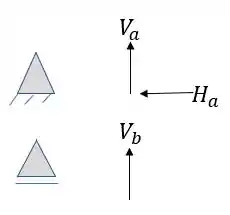
Em que um dos apoios dão resistência horizontal e vertical e o outro apoio da resistência apenas vertical, dando assim, ao nosso problema, 3 incógnitas. Quanto as equações, é simples, basta que lembremos das equações de equilíbrio conhecidas
O que também totaliza 3 equações, ou seja, o número de incógnitas é igual ao número de equações, logo, podemos dizer que a estaticidade da nossa treliça no primeiro caso é isostática.
Passo 3
Agora avaliando ainda a treliça da questão a) precisamos confirmar se ela de fato é uma treliça, partindo do nó mais a direita, iremos numerar dois nós respectivos a nossa escolha
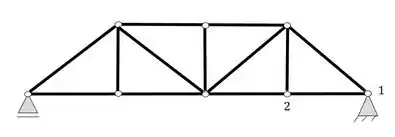
Agora a partir deles devemos ser capaz de definir o próximo nó, que nesse caso será o 3
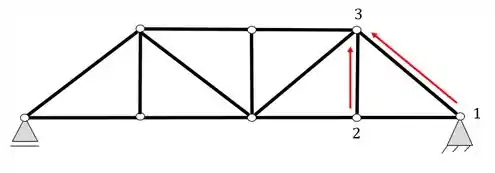
Logo com os nós 1 e 2 foi possível definir o nó 3. Agora usando os nós 2 e 3 vamos tentar definir o nó 4
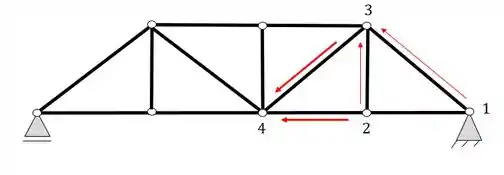
E vamos assim continuar a sequência definindo agora o nó 5 a partir de 3 e 4
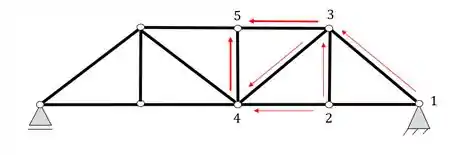
E seguindo a mesma sequência definimos os próximos nós
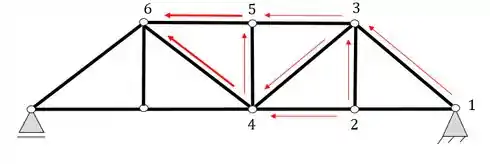
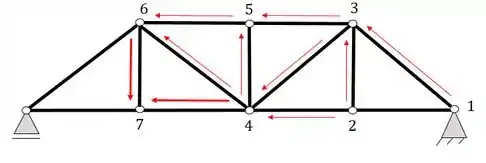
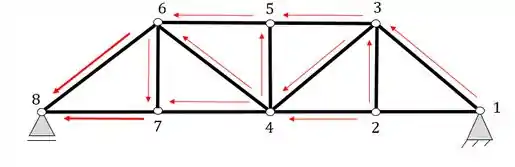
Ou seja, de fato a nossa treliça a) é uma treliça simples e tem equilíbrio do tipo isostático
Passo 4
Vamos agora para a treliça b)
Perceba que os apoios que compõe a trelia b) são exatamente os mesmos apoios da nossa treliça a), logo podemos pular essa parte, porque já sabemos que a nossa treliça b) também é isostática no que se refere aos apoios, vamos então ao mais importante que é avaliar se de fato a nossa treliça é uma treliça.
Mas antes de fazer isso, vamos dividir a nossa treliça grande em treliças mais simples, perceba que podemos encontrar pontos que são mais fáceis de quebrarmos as ligações (veremos melhor como fazer isso na aula de treliças compostas) mas aqui vale apenas dar um spoiler que sempre que formos separar treliças faremos isso nas rótulas. Fazendo uma divisão prévia teremos.
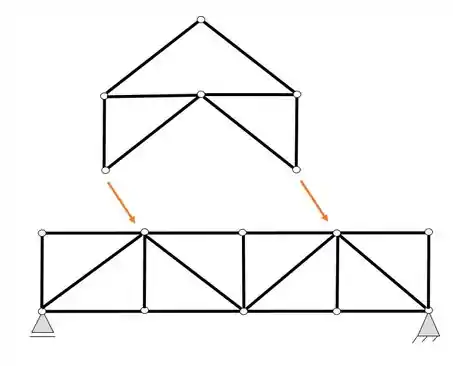
Perceba que a treliça de cima ainda pode ser dividida de forma mais simples como vemos abaixo
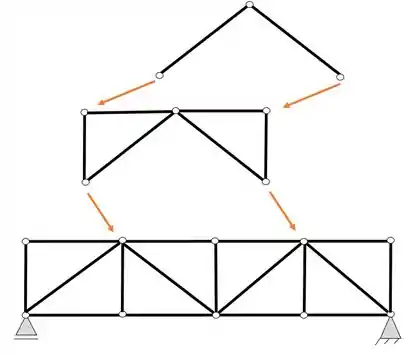
Numerando cada parte teremos
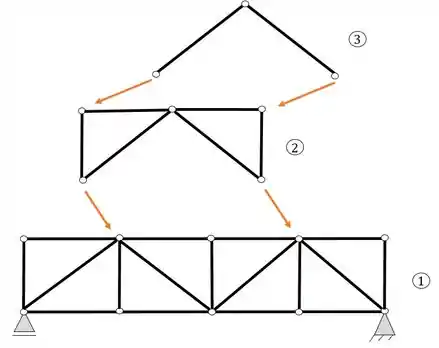
Perceba que em um primeiro momento pode parecer muito complexo definir todos os nós e ver se todas as regras de triangulo estão valendo, mas lembre do seguinte. Pra considerarmos a nossa estrutura como uma treliça, todas as partes que compõem ela, devem ser uma treliça. Podemos chutar que as estruturas 1 e 2 são treliças, mas elas são mais complexas, então vamos começar da estrutura mais simples (a estrutura 3). Se a estrutura 3 não for uma treliça, então toda a nossa estrutura não pode ser classificada como uma treliça, então vamos lá.
Primeiro temos que definir 2 nós respectivos, como está a abaixo
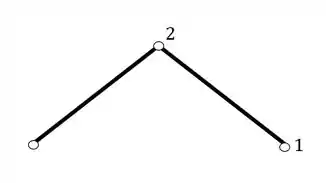
Agora para de fato podermos considerar a nossa a nossa estrutura uma treliça, precisamos chegar no terceiro nó a partir dos dois anteriores
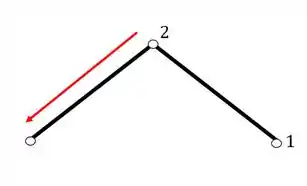
Mas veja que só conseguimos chegar no terceiro nó a partir do nó 2, não tendo essa ligação a partir do nó 1, logo a terceira estrutura subdividida da estrutura principal, não respeita a regra do triangulo, ou seja, a nossa terceira estrutura não é uma treliça, o que nós impede de classificar a estrutura principal como uma treliça. Podemos dizer que as estruturas 1 e 2 de fato são treliças, porém a estrutura 3 não é.
Resposta
- Estrutura de uma treliça
- Não é uma treliça
Estrutura isostática
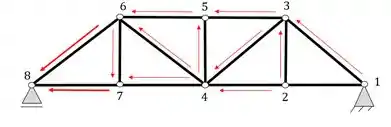
Estrutura isostática