A treliça abaixo representa uma treliça de torres elétricas. Em determinado dia foi entendido que a barra AB possuía um problema de sustentação e deveria ser trocada. Usando seu conhecimento de treliças, determine se a substituição da peça deve ser feita de forma imediata, ou se a manutenção da mesma pode mudar o tipo de estrutura da torre. Se a retirada da barra for causar mudança estrutural, explique a melhor maneira de agira para que isso não ocorra.
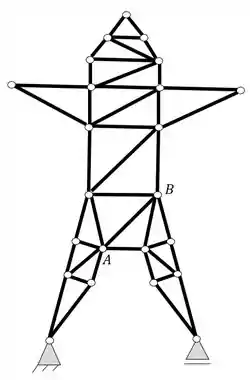
Passo 1
Para sabermos se nossa estrutura é estável devemos fazer duas coisas:
- Primeiro precisamos garantir que a nossa estrutura pode ser definida como uma treliça.
- Se puder ser definida como uma treliça, deveremos refazer a analise, mas agora sem a barra de sustentação. Nesse segundo caso teremos que garantir se a barra de fato irá mudar o estado estrutural da estrutura, e se mudar, deveremos explicar como proceder para evitar isso.
Entendida a forma que iremos proceder, vamos partir para a solução do problema. Bora lá 😊.

Passo 2
Como já sabemos, para definirmos se a nossa estrutura é treliçada, precisamos garantir que conseguiremos determinar todos os nós a partir de 2 nós iniciais, dessa forma, definindo 2 nós iniciais consecutivos, podemos fazer a análise da seguinte maneira
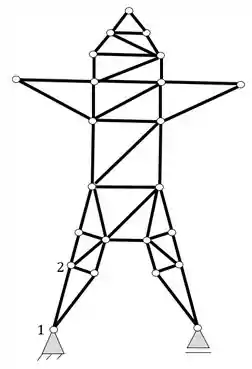
A partir desses 2 nós, conseguimos determinar o terceiro nó, como mostra a figura abaixo
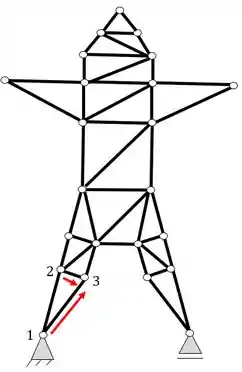
Seguindo o mesmo principio podemos ver abaixo que de fato conseguimos determinar todos os nós a partir dos 2 nós iniciais, logo, de fato a nossa estrutura pode ser considerada uma estrutura do tipo treliçada
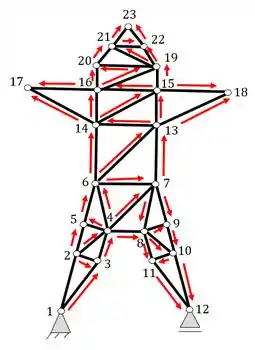
Vamos agora fazer a mesma analise, porém agora, retirando a barra que no enunciado foi dito ter um problema.
Passo 3
Faremos a mesma analise que antes, escolheremos dois nós iniciais e a partir dele iremos ver se conseguimos determinar todos os outros, se não for possível, de fato teremos uma estrutura que não mais é considerada treliçada e nesse caso teremos que dar uma solução ao problema, vamos lá então.
Podemos determinar exatamente os dois nós iniciais que consideramos na figura anterior, porém irei usar nós diferentes para mostrar que podemos fazer essa analise por qualquer lado, desde que comecemos por 2 nós consecutivos. Dessa forma definirei os seguintes nós
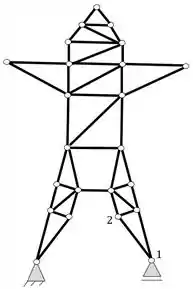
A partir deles podemos definir o nó 3
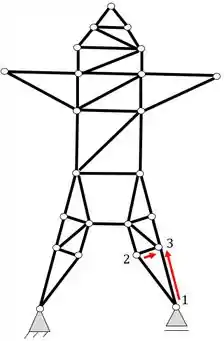
Agora definimos o nó 4
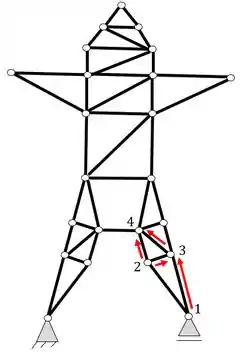
Agora o nó 5
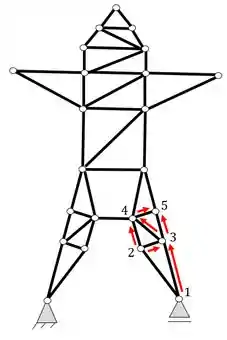
E o nó 6
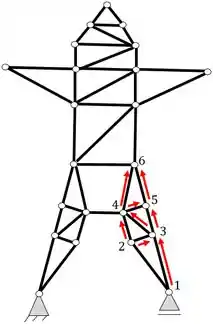
Mas a partir daqui temos um problema, veja que a partir dos nós 4 e 6 é impossível encontrar um próximo nó, pois o que faria a ligação desses nós seria exatamente a barra AB que foi retirada. Ou seja, podemos definir que na verdade a nossa estrutura sofreria riscos caso tirássemos a barra AB, já que a mesma deixaria de ser treliçada como era seu estado anterior. Mas o que podemos fazer pra resolver isso?
Passo 4
Olhando novamente a nossa figura, temos que
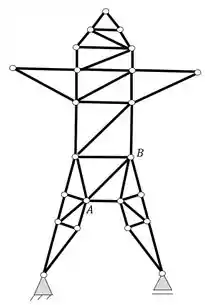
Perceba que a seção que contem a barra AB é uma seção poligonal. Veja também que a seção só possui uma diagonal, ou seja, se possuir mais uma tornaríamos a nossa estrutura hiperestática internamente, logo, o que podemos fazer é, primeiro acrescentar uma diagonal amais no nosso polígono como vemos abaixo
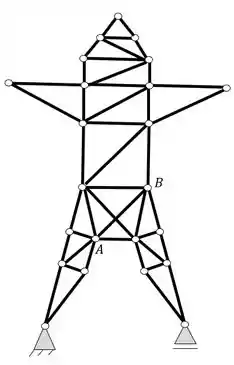
E depois podemos retirar a nossa barra com problemas AB
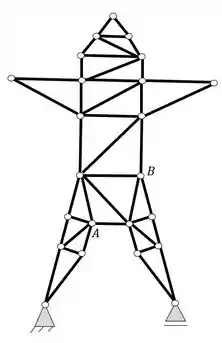
Dessa forma garantimos que a nossa estrutura, tanto antes quanto depois da manutenção é uma estrutura treliçada, o que não colocaria a mesma em risco.
Resposta
Se Retirarmos a barra AB de forma direta da estrutura a mesma se tornará não treliçada, o que colocaria a estrutura em risco de colapso, por isso, o mais indicado, é colocar uma segunda diagonal na seção poligonal com problema e por fim retirar a barra AB, o que garante que a estrutura sempre será treliçada.