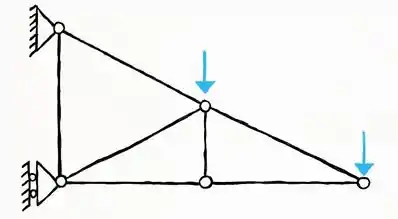
Analise a treliça abaixo e defina se ela pode ser considerada uma treliça isostática.
Passo 1
Primeiro precisamos lembrar que para provarmos que a treliça acima é isostática, precisamos descobrir o número de nós, barras e reações presentes na mesma.
Assim, podemos visualizar que esta treliça é composta por cinco nós (Representados por círculos), sete barras (Segmentos de reta que ligam os círculos) e três reações (Pois nesta treliça temos um apoio de primeiro gênero e um apoio de segundo gênero).
Entre parênteses podemos observar super dicas para você não se confundir na hora determinar o número exato de cada elemento na treliça;
Substituindo na fórmula da Isostática, encontramos:
O que comprova que a treliça acima pode ser considerada como isostática.
Resposta
A treliça é isostática.