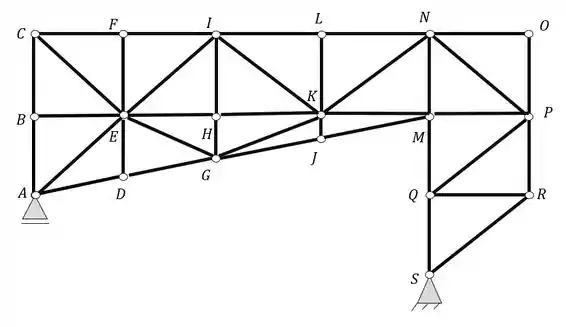
a treliça abaixo apresenta varios estados hiperestáticos internos. Determine quais barras devem ser rompidas para que a mesma se torne uma treliça isostática.
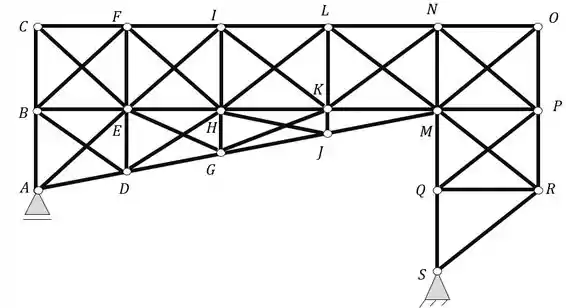
Passo 1
Esse exercício é bem simples mas devemos tomar alguns cuidados.
É bem simples pois vimos um macete na teoria, sabemos que o que torna a nossa estrutura hiperestática internamente é o número de diagonais em um polígono de 4 lados, sabemos que para ser isostático devemos ter apenas 1 diagonal no polígono, tudo que passar de 1 diagonal pode ser retirado sem mais problemas para estrutura.
Logo, para resolvermos o nosso problema, basta fazermos o seguinte
- Pegar todos os setores de 4 lados
- Ver o numero de diagonais
- Tirar a barra que desejar desde que sobre uma barra na diagonal
- Fazer isso em todos os setores de 4 lados
Se fizermos exatamente isso, no fim teremos uma estrutura completamente isostática, tanto externamente quanto internamente. Vamos testar então? bora lá

Passo 2
Como dito vamos começar da esquerda pra direita e de baixo para cima, o nosso primeiro setor está marcado de verde
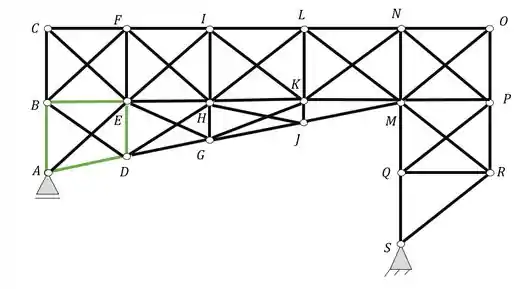
Perceba que podemos tirar tanto a barra AE quanto a barra BD, ambas podem ser retiradas sem mais problemas, nesse caso escolhendo aleatoriamente posso retirar a barra BD e com isso teria
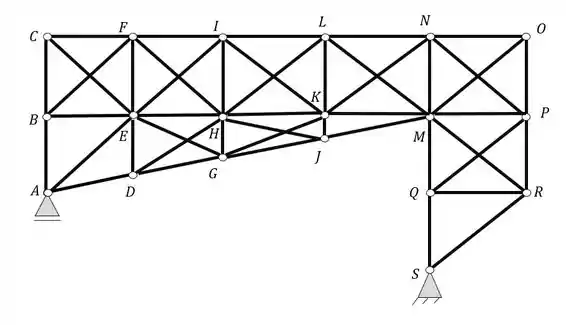
Repetindo esse processo para cada setor poligonal da nossa estrutura teremos que as barras escolhidas para serem retiradas são
BD
DH
HJ
BF
FH
HL
LM
MO
MR
E dessa forma nossa estrutura isostática será
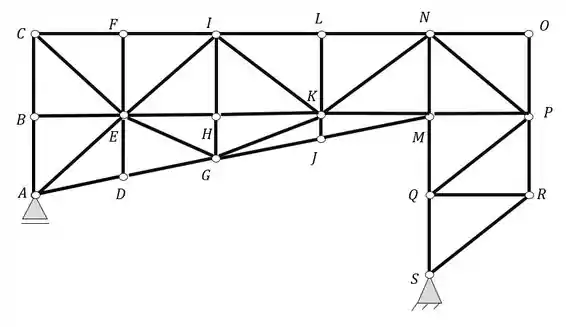
E é só isso o exercício 😊😊😊
Resposta
As barras a serem rompidas são
BD
DH
HJ
BF
FH
HL
LM
MO
MR
E a estrutura isostática será